|
This book (Practical Electron Microscopy and Database) is a reference for TEM and SEM students, operators, engineers, technicians, managers, and researchers.
|
=================================================================================
In order to improve the energy resolution of EEL spectrum, before spectrum deconvolution, scripts (e.g. applied in Gatan Digital Micrograph) can be used to automatically acquire and store each spectrum separately, and then to evaluate and correct the energy drift in each acquisition. [1, 2] After the drift correction, the EEL spectrum can be deconvoluted using software. For instance, some deconvolution techniques are Fourier ratio method, maximum-entropy (ME) [3,4] and Richardson–Lucy (RL) algorithms [5]. In the Fourier ratio method, the "ideal" core-loss spectrum is obtained by inverse Fourier transform. Since the Fourier ratio deconvolution is a high-frequency enhancement technique, high-frequency noise in the core-loss spectrum is substantially amplified. The ME and RL algorithms estimate a predicted spectrum by convoluting it with an observed low-loss spectrum, and thus they are not so significantly affected by high-frequency noise as compared with the Fourier ratio deconvolution technique.
Examples in Figure 2589 shows the effects of energy resolution enhanced by energy-drift correction and deconvolutions in the EEL spectrum of h-BN. The EEL spectra are acquired with an exposure time of 80 ms, a probe current of 100 pA and a high energy-dispersion (0.021 eV ch–1). Figure 2589 (a) shows a blind-sum spectrum with a wide energy spread of 0.48 eV in FWHM (full width at half maximum) due to the energy drift during data acquisition. Figures 2589 (b) shows the improvement by the energy-drift correction, reflecting the inherent high energy-resolution of a cold field emission electron gun (CFEEG). Figures 2589 (c) and (d) show the boron K-edge spectra before and after drift correction, respectively, with π* peak reduced from 1 to 0.52 eV. Figures 2589 (e) and (f) shows further improvement by RL (Richardson-Lucy) and ME (maximum-entropy) deconvolution, respectively.
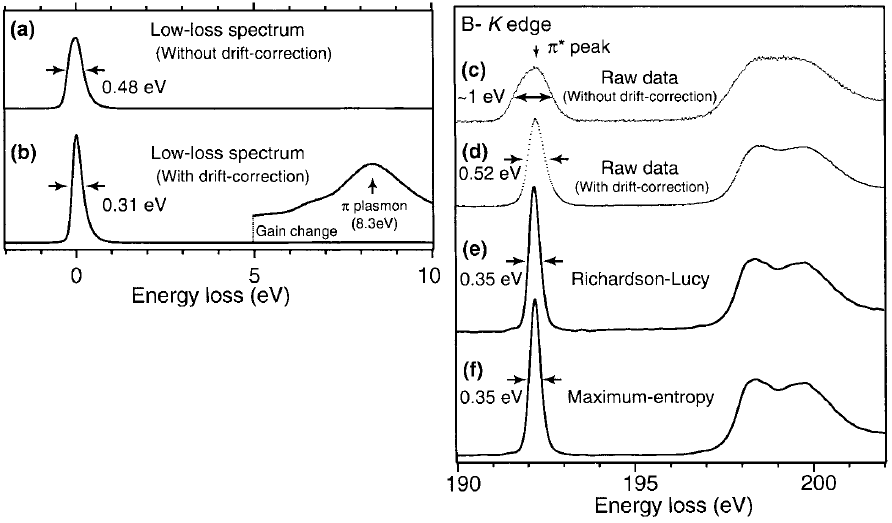
Figure 2589. Low-loss and core-loss spectra of h-BN. (a) and (c) raw spectrum, (b) and (d) spectra after drift correction, and (e) and (f) deconvoluted B K-edge ELNES using RL algorithm and ME algorithm, respectively.
Adapted from [2]
[1] Kimoto K and Matsui Y (2002) Software techniques for EELS to realize
about 0.3 eV energy resolution using 300 kV FEG-TEM. J. Microsc.
208: 224–228.
[2] Koji Kimoto, Kazuo Ishizuka, Teruyasu Mizoguchi, Isao Tanaka and Yoshio Matsui, The study of Al-L23 ELNES with resolution-enhancement software and first-principles calculation, Journal of Electron Microscopy 52(3): 299–303 (2003).
[3] Kuzuo R and Tanaka M (1993) Resolution enhancement of electron
energy-loss spectra using the maximum entropy method. J. Electron
Microsc. 42: 240–243.
[4] Overwijk M H F and Reefman D (2000) Maximum-entropy deconvolution
applied to electron energy-loss spectroscopy. Micron 31: 325–331.
[5] Gloter A, Douiri A, Tencé M, Imhoff D, and Colliex C (2002) Improving
energy resolution of EELS spectra: an alternative to the monochromator
solution. In: Proc. of 15th ICEM, Durban, South Africa, pp. 141–142.
|
