=================================================================================
Kinematic theory describes single scattering of electrons by the electrostatic potential of the TEM sample out of the primary beam into the diffracted beams while the former is negligibly attenuated. In EM (electron microscopy) crystallography, kinematic and quasi-kinematic approximations to the scattering of fast electrons allow for successfully solving and refining of unknown crystal structures, known as “structural electron crystallography”.
One method to quantum scattering is that the wave equation is mathematically converted to an integral form using the Green’s function. This integral equation is then expanded into Born series. As a first-order Born approximation, only the first term of the Born series is used. This is equivalent to assuming the incident electrons are scattered no more than once when penetrating through the specimen, called single, or kinematical, scattering. Using only the first term of the Born series also assumes that the directly transmitted electron wave can be reasonably approximated by the incident wave. In other words, the intensity of the diffracted waves is negligible compared to that of the direct wave. Note that the first-order Born approximation is also equivalent to the Fraunhofer diffraction approximation. Figure 2737 schematically illustrates this quantum scattering applied in electron-microscopy crystallography.
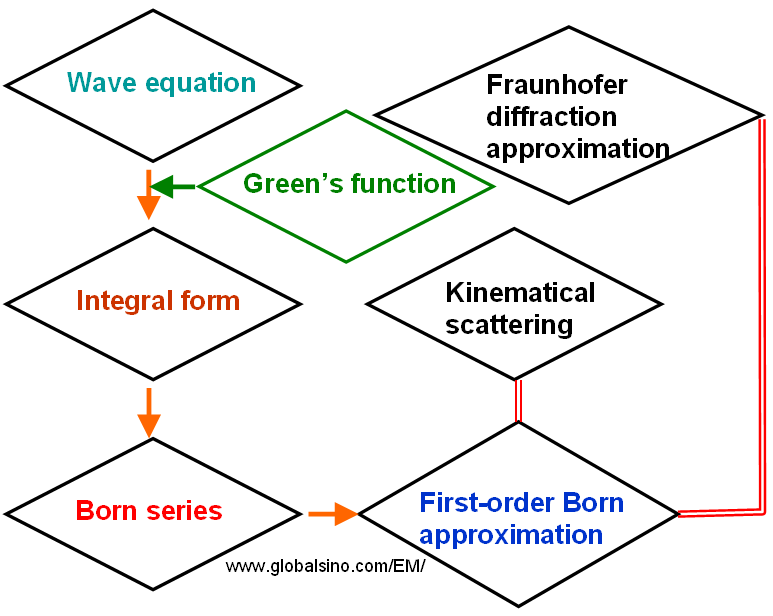
Figure 2737. Schematic illustration of quantum scattering applied in electron-microscopy crystallography.
XRD obeys Friedel's Law because it can be approximately described by kinematical scattering. This limits the number of the space groups of crystals that can be determined by XRD to fifty. For electron diffraction, multiple (dynamical) scattering of the incident electrons in the TEM specimen occurs so that the Friedel's law is broken down, and thus the crystals with all the 230 space groups can be identified.
|
