=================================================================================
In EM (electron microscopy) crystallography, one method to quantum scattering is that the wave equation is mathematically converted to an integral form using the Green’s function. This integral equation is then expanded into Born series. As a first-order Born approximation, only the first term of the Born series is used. This is equivalent to assuming the incident electrons are scattered no more than once when penetrating through the specimen, called single, or kinematical, scattering. Using only the first term of the Born series also assumes that the directly transmitted electron wave can be reasonably approximated by the incident wave. In other words, the intensity of the diffracted waves is negligible compared to that of the direct wave. Note that the first-order Born approximation is also equivalent to the Fraunhofer diffraction approximation. Figure 1964 schematically illustrates this quantum scattering applied in electron-microscopy crystallography.
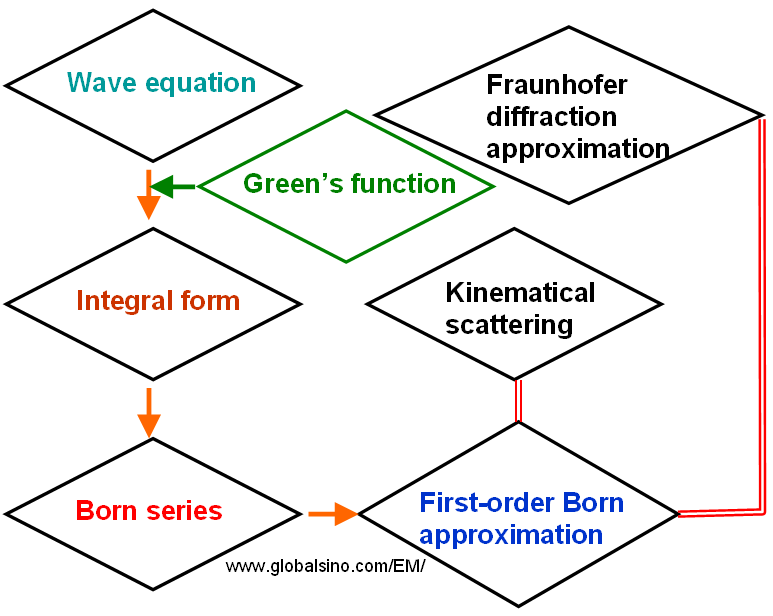
Figure 1964. Schematic illustration of quantum scattering applied in electron-microscopy crystallography.
Because the intensity of Ronchigram, formed at the Fraunhofer diffraction plane, varies significantly with angle, and this variation is a very sensitive function of lens aberrations and defocus [1], Ronchigram is a very useful way to characterize and optimize the electron probe in STEM mode.
Based on the expression of Fraunhofer diffraction one can derive the phase-object approximation (POA) that gives the TEM-specimen transmission function qe(r) as,
 ------------------------------ [1964] ------------------------------ [1964]
where,
σ -- The interaction constant,
ϕp(r) -- The projection of the electrostatic potential of the specimen along the direction of the electron beam.
[1] J.M. Cowley, Electron diffraction phenomena observed with a high resolution STEM instrument, J. Electron. Microsc. Tech. 3 (1986) 25-44.
|
