=================================================================================
Assuming the TEM specimen is a perfect crystal, in two beam condition the intensity (Ig) of diffracted electron beam can be given by (based on dynamical theory),
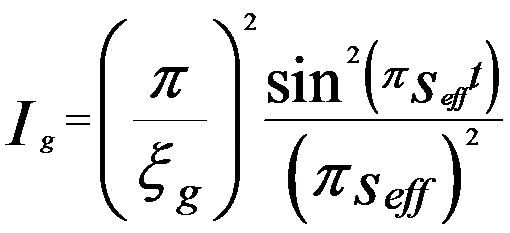 ------------------------- [4132a] ------------------------- [4132a]
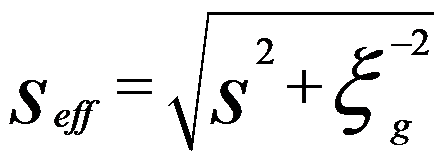 ------------------------- [4132b] ------------------------- [4132b]
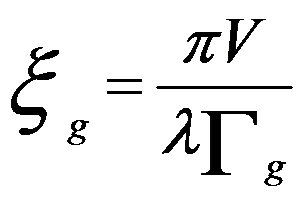 ------------------------- [4132c] ------------------------- [4132c]
where,
seff -- Effective deviation parameter
ξg -- Extinction distance
V -- Volume of the unit cell
λ -- Electron wavelength
Γg -- Structure factor of the unit cell for diffraction g
s -- Deviation parameter
t -- Crystal thickness
Equation 4132a for dynamical theory is valid when the TEM sample is thick and s is about zero, but is not valid in kinematical theory. From Equation 4132c we can know that the extinction distance decreases with increase of scattering (increase of Γg). When s is equal to zero (exact Bragg condition) we have seff = 1/ξg, meaning the transmitted (I0) and diffracted (Ig) intensities has a periodicity of ξg in TEM specimen depth indicated in Figure 4132 in two beam condition. Here, I0 = 1 - Ig in two beam condition.
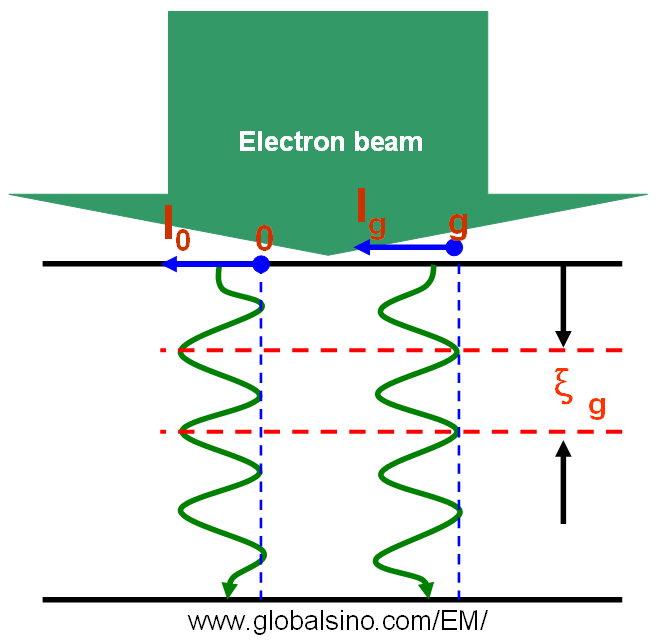
Figure 4132. The diffracted intensity (Ig) showing a periodicity of ξg in TEM
specimen depth in two beam condition. Ig is the intensity of transmitted beam.
The exchange of intensity between the forward and diffracted beams in dynamical theory is called pendellösung. Pendellösung is not a kinematical effect because it does not allow such large change in intensity.
In EM (electron microscopy) crystallography, one method to quantum scattering is that the wave equation is mathematically converted to an integral form using the Green’s function. This integral equation is then expanded into Born series. As a first-order Born approximation, only the first term of the Born series is used. This is equivalent to assuming the incident electrons are scattered no more than once when penetrating through the specimen, called single, or kinematical, scattering. Using only the first term of the Born series also assumes that the directly transmitted electron wave can be reasonably approximated by the incident wave. In other words, the intensity of the diffracted waves is negligible compared to that of the direct wave.
|
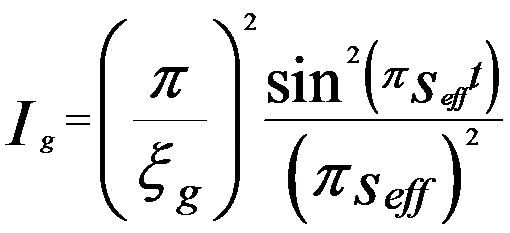 ------------------------- [4132a]
------------------------- [4132a] 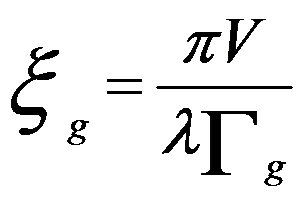 ------------------------- [4132c]
------------------------- [4132c] 