|
This book (Practical Electron Microscopy and Database) is a reference for TEM and SEM students, operators, engineers, technicians, managers, and researchers.
|
=================================================================================
In coma case, most of its intensity distributes on one side and a “comet tail” on the other.
Figure 4239a shows typical Ronchigrams taken at the edge of an amorphous carbon film. At defoci (defined by z-height), there is a distance between the electron cross-over and the point on the specimen along the optic axis. At large underfocus, electron rays at all angles cross the optic axis after the specimen and it shows a shadow image of the specimen edge. At small underfocus, low-angle rays cross the optic axis after the specimen, while high-angle rays cross before the specimen due to spherical aberration. Therefore, the shadow image changes in magnification as a function of the angle. The low-angle asymmetry indicates the presence of astigmatism. At Gaussian focus, the lowest-angle rays cross the axis at the specimen, while higher-angle rays cross before the specimen due to the spherical aberration. The coma free axis is defined at this focus and all alignment and positioning of detectors and apertures can be performed with respect to the low-angle “disk”. Defocus and spherical aberration can effectively cancel each other at those lowest angles. Axial astigmatism can be accurately corrected by using the stigmator coils, resulting in circularly symmetric Ronchigram features. At overfocus, rays at all angles cross the axis before the specimen.
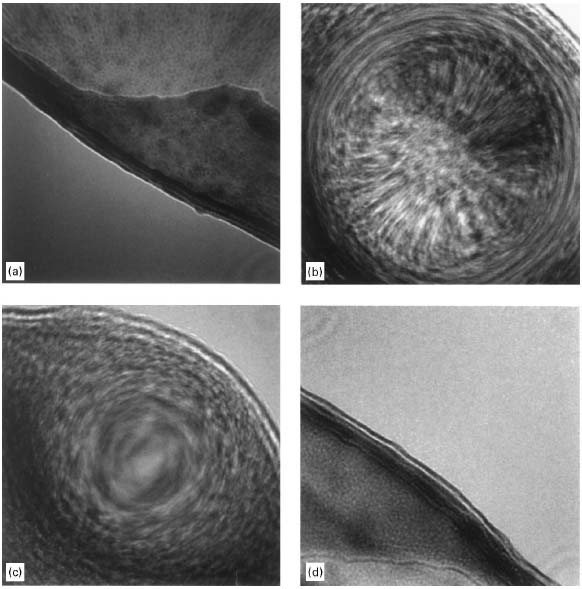
Figure 4239a. Ronchigrams of a thin amorphous carbon (C) film at: (a) Large underfocus, (b) Small underfocus, (c) Gaussian focus, and (d) Overfocus.
[1]
In TEM observations, axial coma can easily be distinguished from twofold astigmatism, because the axial coma pattern does not change its intensity orientation from overfocus to underfocus.
Figure 4239b shows the schematic comparison of Zemlin (diffractogram)-tableau characteristics for the axial aberrations up to third orders. First-order aberration (e.g. defocus and twofold astigmatism, A1) shows the elliptical distortion even without electron beam tilting because the impact of first-order aberrations does not depend on the tilt angle. For the aberrations of higher orders (n≥2), such as second-order axial coma B2, three-fold astigmatism A2, third-order spherical aberration C3 (>0), third-order star aberration S3 and four-fold astigmatism A3, there is no elliptical distortion observable for the un-tilted case. In these cases, only at illumination tilts the characteristic distortion due to the aberrations becomes discernible. Note that the higher-order aberrations have equal symmetries to the ones in Figure 4239b as discussed in page3740.
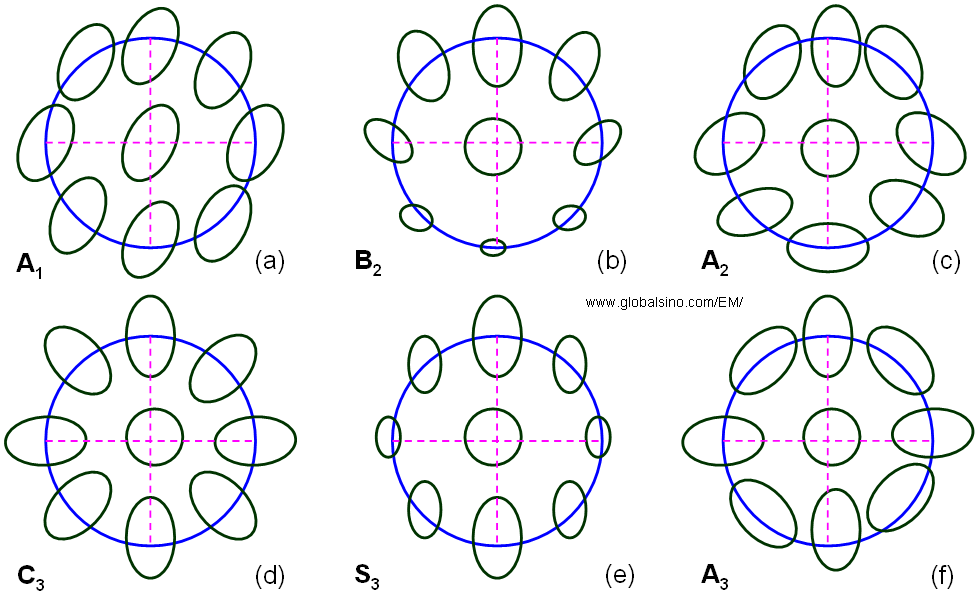
Figure 4239b. Schematic representation of Zemlin (diffractogram)-tableau characteristics for the axial aberrations up to third order.
[1] E.M. James, N.D. Browning, Practical aspects of atomic resolution imaging and analysis in STEM, Ultramicroscopy 78 (1999) 125-139.
|

