=================================================================================
The distribution of the magnetic field on the optic z axis can be evaluated by different models. However, the Glaser field offers the some advantages, for instance, the most important properties, the positions of foci and principal planes can be calculated straightforwardly. On this theory, Glaser’s “Glockenfeld” (also called bell-shaped field as shown in Figure 4279a) gives the approximate distribution of the magnetic field [1]:
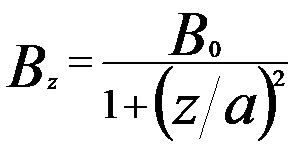 -------------------------- [4279a] -------------------------- [4279a]
where,
B0 -- The maximum field in the lens center
2a -- The full-width at half-maximum
(FWHM)
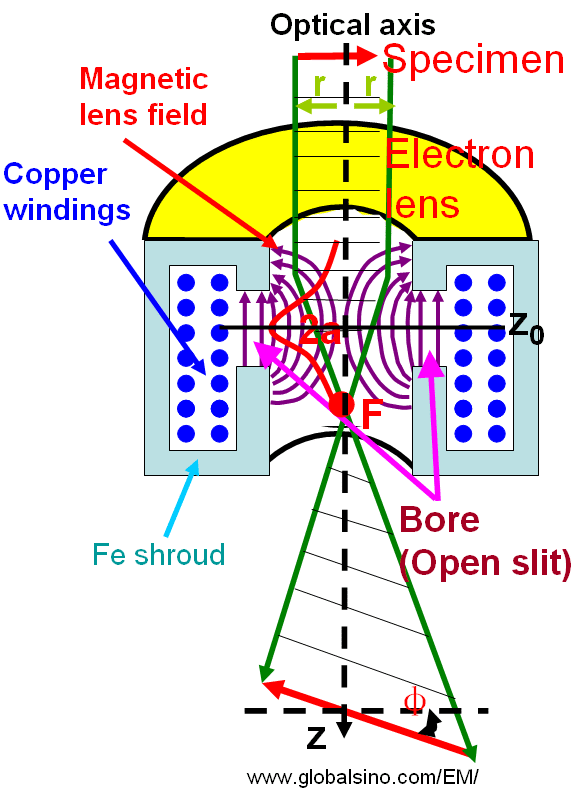
Figure 4279a. Rotationally symmetric magnetic fields and electron lenses.
By introducing dimensionless coordinates y = r/a and x = z/a = cot φ (where we have the variable φ varying from π (z = −∞) to π/2 (z = 0) and then to 0 (z = +∞).), by following the theory of trajectories of electron in electron lenses,
and by assuming a ray passing through a point P0(y0, φ0) in front of the lens, a image point P1(y1, φ1) can be theoretically obtained,
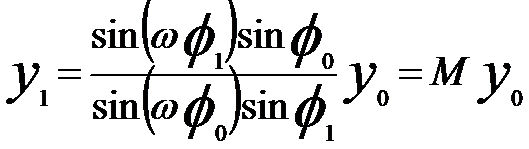 -------------------------- [4279b] -------------------------- [4279b]
where,
M -- Magnification
ω -- Lens strength,
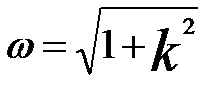 ---------------------------------- [4279c] ---------------------------------- [4279c]
Therefore, we can have,
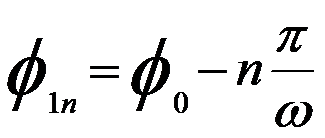 -------------------------- [4279d] -------------------------- [4279d]
This equation indicates that more than one image point can occur in strong lenses. However, The second focus (n = 2) will not be possible until ω ≥ 2 or k2 ≥ 3. Figure 4279b shows the electron trajectories incident parallel to the axis for increasing values of lens strength (ω).
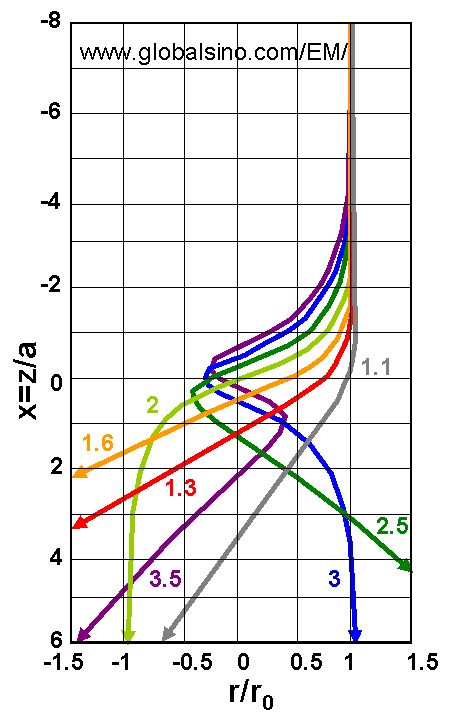
Figure 4279b. The electron trajectories incident parallel to the axis for increasing
values of lens strength (ω). Adapted from [2]
Glaser’s famous bell-shaped model suggested that in order to attain the minimum focal length and the minimum aberrations of a magnetic lens used in a TEM the specimen should be put at the middle of the gap of a pair of symmetrical polepieces [3], e.g. called objective polepiece.
[1] W. Glaser: Strenge Berechnung magnetischer Linsen der Feldform H =
H0/[1 + (z/a)2]. Z. Phy. 117, 285 (1941).
[2] W. Glaser: Grundlagen der Elektronenoptik (Springer, Wien, 1952).
[3] Cosslett, V. E. 1991. Fifty years of instrumental development of the electron microscope, in Advances in Optical and Electron Microscopy, Barer, R. and Cosslett, V. E. Eds., Academic Press, London, 215–267.
|
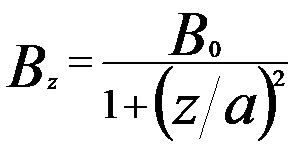 -------------------------- [4279a]
-------------------------- [4279a] 
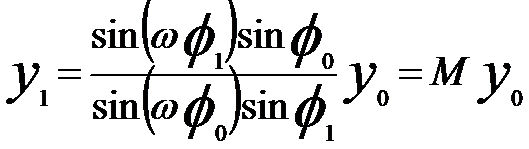 -------------------------- [4279b]
-------------------------- [4279b]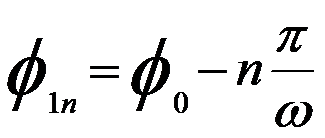 -------------------------- [4279d]
-------------------------- [4279d]