=================================================================================
The theory of lattice-fringe visibility developed by Fraundorf et al. [1] calculates the probability of detecting a set of lattice fringes, e.g. for a randomly oriented polycrystalline materials and nanocrystals, by employing the concept of lattice-fringe visibility bands. The visibility is a function of the crystalline orientation of the TEM specimen. As shown in Figure 2730a, a visibility band in green illustrates the visibility of a set of parallel lattice planes of a spherical crystal at point O. Such a band defines that the lattice fringes are visible when the electron beam direction lies in it. In other words, this visibility band will be symmetric about a great circle, running through A. The maximum visibility-band half-width in kinematic approximation is given by,
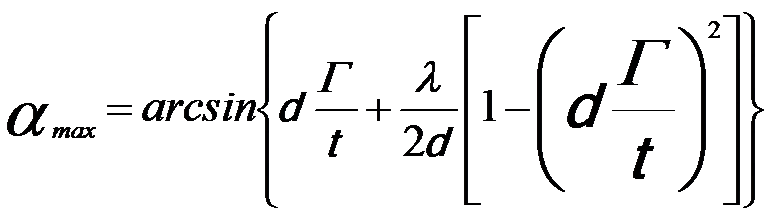 ------------------------ [2730a.a] ------------------------ [2730a.a]
where,
t -- The crystal thickness,
Γ -- A “visibility” factor, taking into account non-ideal imaging condition, which is on the order of 1 that empirically accounts for the signal-to-noise ratio in the method used to detect fringes, (e.g. Γ ≈ 0.8 for Au/Pd nanoparticles)
λ -- The wavelength of the electrons,
d -- The spacing of the lattice planes.
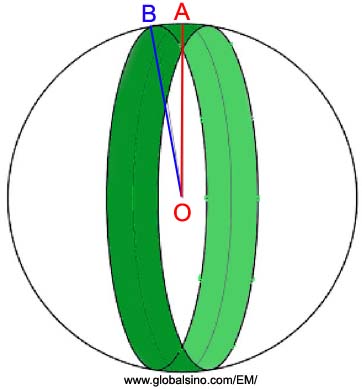
Figure 2730a. Schematic illustration of lattice-fringe visibility band for a set of lattice planes parallel to the great circle passing through A. The sphere represents all possible electron beam directions incident on the specimen (O). The lattice fringes are visible when the electron beam passes through the visibility band. The visibility-band half-width, ∠AOB, is equal to αmax. The lattice fringes disappear as the electron beam is tilted by an angle greater than αmax. The solid angle for the visibility band is 4π·sinαmax [1].
For thin specimens and the small λ/d of typical electron microscopes, Equation 2730a.a can be simplified to,
 ------------------------ [2730a.b] ------------------------ [2730a.b]
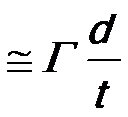 ------------------------------------------------ [2730a.c] ------------------------------------------------ [2730a.c]
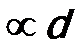 -------------------------------------------------------- [2730a.d] -------------------------------------------------------- [2730a.d]
As shown by the first term in Equation 2730a.c, the maximum visibility-band half-widths are proportional to d-spacing over thickness, rather than to wavelength over d-spacing as in the cases of electron-channeling pattern [2], Kikuchi [3], bend-contour [4,5], and backscatter-electron diffraction [6] bands in thicker TEM specimens.
The solid angle (Ω), for the intersection of two lattice-fringe visibility bands with half-widths of αmax and βmax intersecting at an angle γ, is given by,
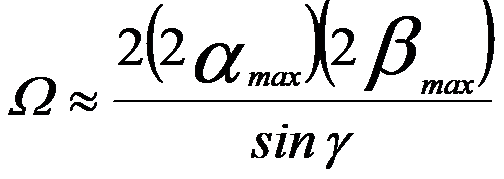 ------------------------ [2730b] ------------------------ [2730b]
Therefore, the probability, Puvw, of detecting a family of zone axe <uvw> is given by,
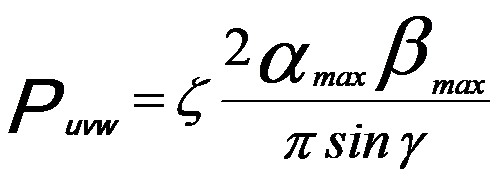 ------------------------ [2730c] ------------------------ [2730c]
where,
ζ -- The multiplicity.
An improvement of continuous contrast transfer (e.g. with aberration correction) results in an increase of the number of visibility bands on a map. For instance, Figure 2730b show the difference of the fractions of visibility band maps for an 8-nm Al nanocrystal at point resolutions of 1 and 0.6 Å, respectively. Therefore, the lattice parameter determination will be easier and more accurate because of the improvement of TEM resolution.
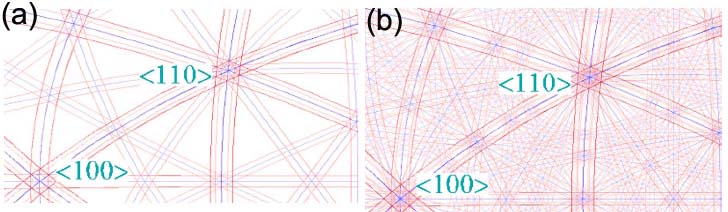
Figure 2730b. Visibility band map fractions for an 8-nm Al crystal at point resolutions of (a) 1 Å and (b) 0.6 Å.
Adapted from [1]
On the other hand, the grain (or crystal) size decrease causes visibility-band broadening.
Crystalline specimens have to be tilted in a goniometer in TEM in order to:
i) Observe lattice fringes and crystal structures.
ii) Determine the crystal orientation.
iii) Observe diffraction contrast of lattice defects with certain Bragg reflections or known orientation.
iv) Determine the Burgers vector of lattice defects.
[1] P. Fraundorf, W. Qin, P. Moeck, and E. Mandell. Making sense of nanocrystal lattice fringes. Journal of
Applied Physics, 98:114308, 2005.
[2] D. C. Joy, in Quantitative Scanning Electron Microscopy,
edited by D. B. Holt, M. D. Muir, L. M. Boswarva, and P. R. Grant (Academic Press, New York, 1974).
[3] S. Nishikawa and S. Kikuchi, Nature 121, 1019 (1928).
[4] P. Hirsch, A. Howie, R. B. Nicholson, D. W. Pashley,
and M. J. Whelan, Electron Microscopy of Thin Crystals
(Robert E. Krieger Publishing Company, Huntington, New
York, 1977), 2nd ed.
[5] L. Reimer, Transmission electron microscopy: Physics
of image formation and microanalysis (Springer, Berlin,
1997), 4th ed.
[6] J. A. Venables and C. J. Harland, Phil. Mag. 27, 1193
(1973).
|
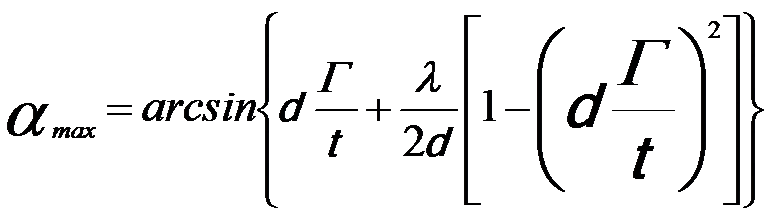 ------------------------ [2730a.a]
------------------------ [2730a.a] 
 ------------------------ [2730a.b]
------------------------ [2730a.b] 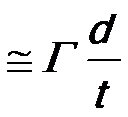 ------------------------------------------------ [2730a.c]
------------------------------------------------ [2730a.c]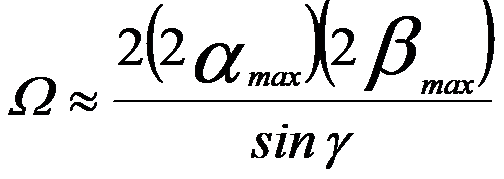 ------------------------ [2730b]
------------------------ [2730b] 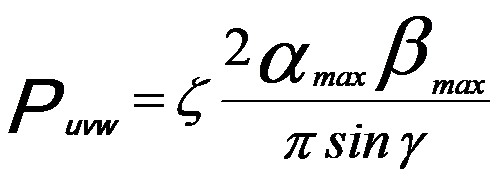 ------------------------ [2730c]
------------------------ [2730c] 