=================================================================================
Symmetry describes how a pattern repeats within a crystal. Space groups represent the ways that the macroscopic and microscopic symmetry elements (operations) can be self-consistently arranged in space. There are totally 230 space groups. The space groups add the centering information and microscopic elements to the point groups.
Symmetry operators are the motions that allow a pattern to be transformed from an initial position to a final position and the initial and final patterns are indistinguishable. The symmetry operators are:
i) Translation.
ii) Reflection.
iii) Rotation.
iv) Inversion (center of symmetry).
v) Roto-inversion (Rotation followed by inversion through the origin).
vi) Roto-reflection.
vii) Glide (translation plus reflection).
viii) Screw (rotation plus translation).
Figure 3556 schematically shows the relationship between the 7 crystal systems, 14 Bravais Lattices, 32 point groups, and 230 space groups. Table 3556a also lists the symmetry operations and symmetry elements. Table 3556b shows the relation between three-dimensional crystal families, crystal systems, and lattice systems.
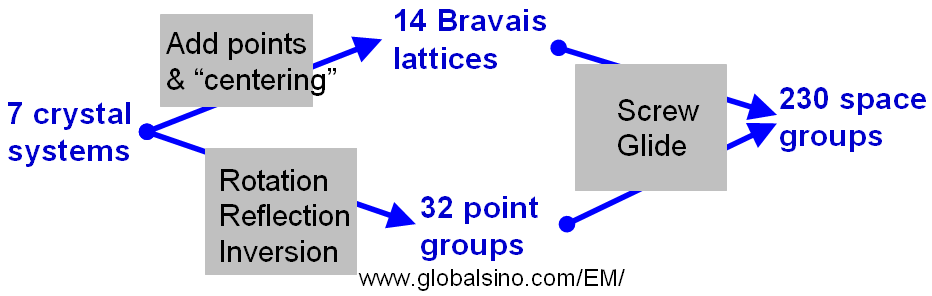
Figure 3556. The relationship between the 7 crystal systems,
14 Bravais Lattices, 32 point groups, and 230 space groups.
Table 3556a. Symmetry operations and symmetry elements
| |
Symmetry element |
Symmetry operation |
| E |
|
Identity [1] |
| Cn |
n-fold symmetry axis |
Rotation by 2π/n |
| σ |
Mirror plane |
Reflection |
| i |
Center of inversion |
Inversion |
| Sn |
n-fold axis of improper rotation [2] |
Rotation by 2π/n followed by reflection perpendicular to rotation axis |
[1] The symmetry element can be thought of as the whole of space.
[2] The equivalences S1 = σ and S2 = i.
Table 3556b. The relation between three-dimensional crystal families, crystal systems, and lattice systems.
Crystal
family |
Crystal
system |
Required
symmetries
of point group |
Point
group |
Space
group |
Bravais
lattices |
Lattice
system |
| Triclinic |
None |
2 |
2 |
1 |
Triclinic |
Monoclinic
|
1 two-fold axis of rotation or 1 mirror plane |
3
|
13
|
2
|
Monoclinic |
Orthorhombic |
3 two-fold axes of rotation or 1 two-fold axis of rotation and two mirror planes |
3 |
59 |
4 |
Orthorhombic |
Tetragonal |
1 four-fold axis of rotation |
7 |
68 |
2 |
Tetragonal |
| Hexagonal |
Trigonal |
1 three-fold axis of rotation |
5 |
7 |
1 |
Rhombohedral |
| 18 |
1 |
Hexagonal |
| Hexagonal |
1 six-fold axis of rotation |
7 |
27 |
Cubic
|
4 three-fold axes of rotation |
5 |
36 |
3 |
Cubic |
| Total: 6 |
7 |
|
32 |
230 |
14 |
7 |
With stereographic projections, we can easily visualize crystallographic features:
i) Crystal symmetry.
ii) Slip planes and directions.
iii) Crystal planes and orientation relationships.
iv) Grain orientations.
|
