=================================================================================
Numerical simulations modeling TEM (transmission electron microscopy) and STEM images have mainly been traditionally performed using the two methods:
i) Multislice simulation (MS),
ii) Bloch wave approaches.
For instance, both models can be employed to calculate the exit-surface elastic wave function. In STEM analysis, the effect of the beam–specimen interaction in modifying the probe wave function into the sample exit wave function can be modeled using either the Bloch wave approach [3,4] or a multislice approach. [5,6]
The MS method of TEM images simulates images from a crystal model. The multislice method is based on performing propagation steps as a multiplication in reciprocal space but phase grating steps as a multiplication in real space.
By splitting the crystalline TEM sample into many thin slices (typically ~ 0.2 nm thick per slice) perpendicular to the electron beam as shown in Figure 3670a we can use the weak phase object approximation (WPOA) to extract the effect of the interaction of an electron wave with each slice. A free space propagator is applied after the electron wave has passed through one slice and before reaching the next slice and so on until it has passed through all the slices which make up the crystalline TEM sample. Therefore, the simulated electron wave function is the object wave function of the crystal model and it is possible to add the effects of aberrations into and convert the wave function into an image. Figure 3670a gives the multislice approximation converts a specimen (a) into many thin slices (b). The electron wave is incident on the top of the specimen, transmits through the specimen (or many slices in the model (b)) and exits on the bottom. Based on WPOA, each slice causes a simple phase shift of the electron wave.
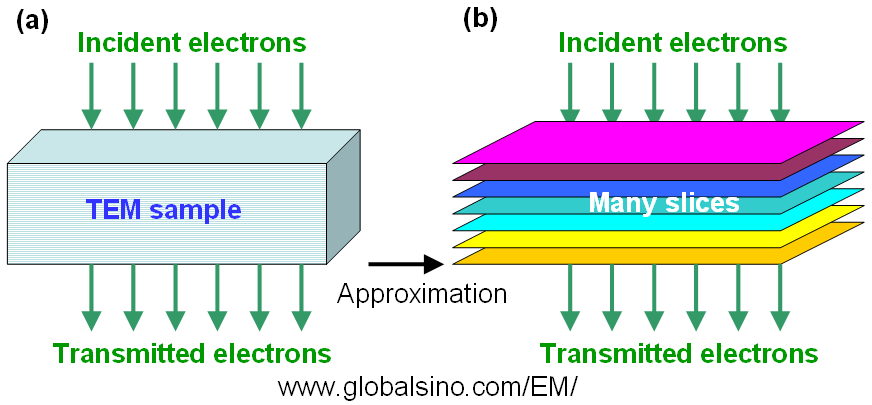
Figure 3670a. (a) Electron wave passing a TEM sample and (b) The multislice approximation.
Even though each individual slice can be represented by the WPOA modeling the simulation as a whole will still include non-linear effects because of using many slices and allowing the electron wave to propagate between them. Furthermore, the images obtained by the simulation are still different from the real TEM images and will show a significantly higher contrast.
As an example, Figure 3670b shows the effects of a [100] oriented Si (silicon) lattice on a 100 keV incident plane wave, calculated using multislice method [1]. In this model, the electron beam is alternately transmitted through a thin slice and propagated to the next slice with a thickness of 1.3575 Å. During the propagation, the phase of the plane wave is shifted by the projected atomic potential. The peaks in the images correspond to the position of the atomic columns (channeling peaks). Note that there is a rapidly oscillating background in the electron wave intensity.
![Calculated electron intensity |ψ(r)|2 as the incident electrons pass through a [100] oriented Si lattice at depths of (a) 10 Å, (b) 100 Å, and (c) 200 Å.](image1/4152dd.gif)
Figure 3670b. Calculated electron intensity |ψ(r)|2 as the incident electrons pass through a [100] oriented Si lattice at depths of (a) 10 Å, (b) 100 Å, and (c) 200 Å. The positions labeled Si are the atom column positions.
Adapted from [2]
[1] E.J. Kirkland, Advanced Computing in Electron Microscopy,
Plenum Press, New York, 1998.
[2] Earl J. Kirkland, Some effects of electron channeling on electron energy loss spectroscopy, Ultramicroscopy 102 (2005) 199–207.
[3] Nellist P, Pennycook SJ. Ultramicroscopy 1999;78:111–24.
[4] Peng Y, Nellist PD, Pennycook SJ. J Electron Microsc 2004;53:257–66.
[5] Kirkland EJ, Loane RF, Silcox J. Ultramicroscopy 1987;23:77–96.
[6] Cowley JM, Moodie AF. Acta Crystallogr 1957;10:609–19.
|
