=================================================================================
The accurate determination of the spherical aberration (Cs) coefficients is very important to many applications of EM techniques, such as electron holography [1,2], image processing and deconvolution [3], and electron crystallography of proteins [4]. The spherical aberration coefficient of EMs can be determined by Krivanek model [5], statistic method [6], and electron-beam-tilt technique [7]. An efficient way for processing the Cs determinations has recently been performed by slow scan charge-coupled device (SSCCD) camera system. For instance, the Cs or residual Cs after aberration corrections in STEM and TEM can be measured by the segmental Ronchigram autocorrelation function matrix (SRAM) method [8] and by the diffractogram tableau method [9, 10], respectively.
Under axial illumination conditions it is not possible to measure all aberration coefficients. In this case, only the defocus and the twofold astigmatism can be determined by the defocus-based techniques. The other aberration coefficients, e.g. spherical aberration, need to be provided by the microscope manufacturer or to be determined by different methods. However, those aberration coefficients, such as the axial coma and the threefold astigmatism, cannot be ignored at high spatial resolutions approaching 0.1 nm. Therefore, the measurements of the other aberration coefficients should be done by other methods such as tilting the illumination. Note that we need to realize that tilting illumination also changes the defocus, astigmatism, and the original aberrations.
Figure 3736 shows the schematic comparison of Zemlin (diffractogram)-tableau characteristics for the axial aberrations up to third orders. First-order aberration (e.g. defocus and twofold astigmatism, A1) shows the elliptical distortion even without electron beam tilting because the impact of first-order aberrations does not depend on the tilt angle. For the aberrations of higher orders (n≥2), such as second-order axial coma B2, three-fold astigmatism A2, third-order spherical aberration C3 (>0), third-order star aberration S3 and four-fold astigmatism A3, there is no elliptical distortion observable for the un-tilted case. In these cases, only at illumination tilts the characteristic distortion due to the aberrations becomes discernible. Note that the higher-order aberrations have equal symmetries to the ones in Figure 3736 as discussed in page3740.
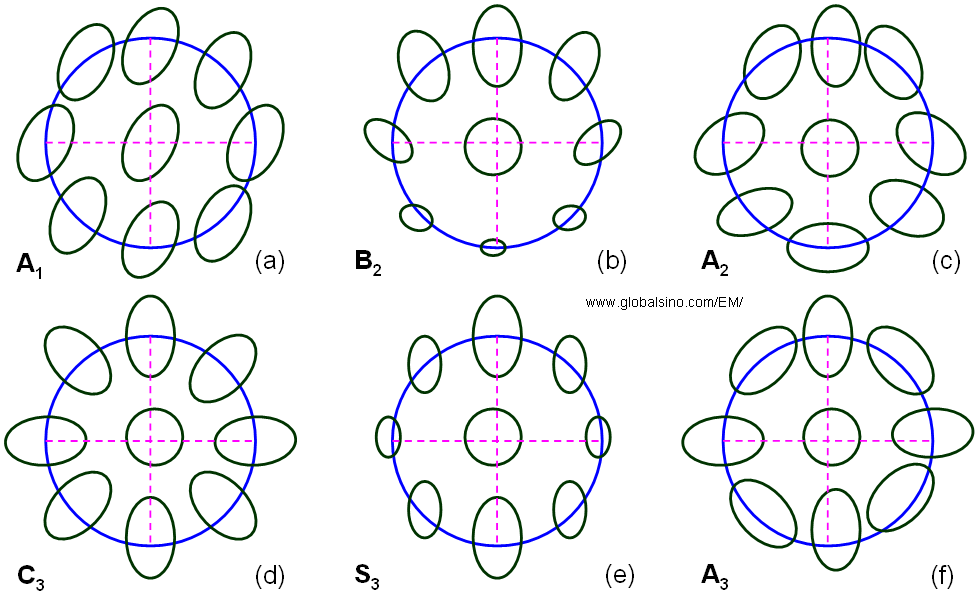
Figure 3736. Schematic representation of Zemlin (diffractogram)-tableau characteristics for the axial aberrations up to third order.
[1]. Liehte, H., Parameters for high-resolution electron holography, Ultramicroscopy, 1993, 51, 15.
[2]. Peng, L.-M., Ren, G., Duan, X. F., Samplling theorem and digital electron microscopy, J. Chinese Electron Microscopy Society (in Chinese), 1996, 15(2-4), 117.
[3]. Li, F. H., Combination of high resolution electron microscopy and electron diffraction in crystal structure determination, J. Chin. Electr. Microsc. Soc., 1996, 1592-4, 143.
[4]. Baumeister, W., Typke, D., Electron Crystallography of Proteins, State of the Art and Strategies for the Future, MSA Bulletin, 1993, 23(1), 11.
[5] Krivanek, O. L., A method for determing the coefficient of spherical aberration from a single electron micrograph, Optik, 1976, 45(1): 97.
[6] Coene, W. M. J., Deneteneer, T. J. J., Improved methods for the determination of the spherical aberration coefficient in high-resolution electron microscopy from micrographs of an amorphous object, Ultramicroscopy, 1991, 38, 225.
[7] Koster, A. J., de Jong, A. J., Measurement of the spherical aberration coefficient of transmission electron microscopes by beam-tilt-induced image displacements, Ultramicroscopy, 1991, 38, 235
[8] Sawada H, Sannomiya T, Hosokawa F, Nakamichi T, Kaneyama T,
Tomita T, Kondo Y, Tanaka T, Oshima Y, Tanishiro Y, and Takayanagi
K (2008) Measurement method of aberration from Ronchigram by
autocorrelation function. Ultramicroscopy 108: 1467–1475.
[9] Zemlin F, Weiss K, Schiske P, Kunath W, and Herrmann K H (1978)
Coma-free alignment of high resolution electron microscopes with
the aid of optical diffractograms. Ultramicroscopy 3: 49–60.
[10] Uhlemann S and Haider M (1998) Residual wave aberrations in the
first spherical aberration corrected transmission electron microscope.
Ultramicroscopy 72: 109–119.
|
