=================================================================================
For a perfectly coherent illumination, the resulting phase contrast transfer function continues to oscillate between +1 and -1 even at very large spatial frequencies. Therefore, the contrast transfer function is given by,
T(k) = D(k) sinχ(k) ----------------------------- [3879a]
where,
sin χ(k) -- Oscillating part, which determines the contrast of the image
χ(k) -- Contrast transfer function (CTF)
k -- Represented by |g| in Equations 4236
D(k) -- Envelope function, which dampens the amplitudes of the high
resolution components, given by,
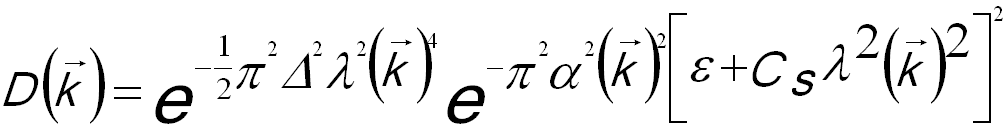 -- [3879b] -- [3879b]
where,
α -- The electron beam convergence
Δ -- The defocus spread
The envelope function represents the attenuation of the wave transfer function due to limited coherence. The first exponential term in Equation 3879b is due to the limited temporal coherence originated from the energy spread of the electrons, which induces a defocus spread Δ because of the chromatic aberration. The second term originates from the angular spread α of the electrons incident at any specific point in the object plane because of the limited spatial coherence originated from the finite source size.
For real TEMs, the phase contrast transfer function is limited by a number of factors: i) Variation in electrical currents in the lenses; ii) Variation in accelerating voltage and gun emission; iii) Attenuation in the CCD camera; iv) Slightly nonparallel illumination; and v) Specimen drift and vibration. All these limits can be described by envelope functions, D, which will gradually dampen the phase contrast transfer function and eventually reduce it below the noise at some spatial frequency. The first three factors depend on the inherent properties of the microscope. For all modern microscopes this significant decrease happens at higher spatial frequencies than the point to point resolution and defines the information limit of the microscope beyond which no information is transferred at all.
|
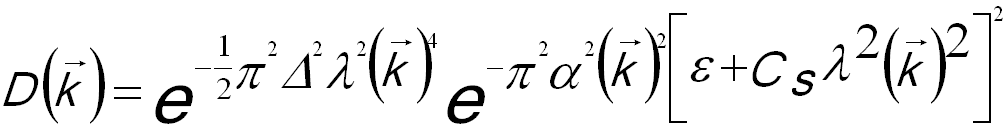 -- [3879b]
-- [3879b]