=================================================================================
Based on the Lorentz model, the interband bulk plasmon peak energy of the i-th oscillator is given by,
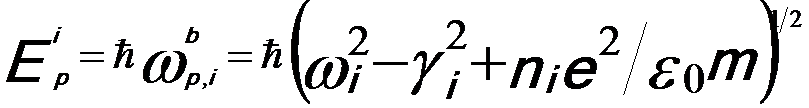 ------------------------- [2313a] ------------------------- [2313a]
where,
ħωi -- The plasmon excitation energy;
γi -- The dumping factor;
ni -- The density of the valence electrons contributing to the plasmon excitation;
e -- The electron charge;
ε0 -- The dielectric constant in the vacuum.
However, perovskite type ferroelectric and high-k dielectric materials, such as BaTiO3 and SrTiO3, normally show only one interband plasmon peak [1–4].
The interpretation of the features of low-loss regions in EELS from free-electron metals is fairly straightforward because the signals arise mainly from bulk and surface plasmon excitations and the energies of the peaks from bulk (Ebulk) and surface (Esurface) plasmon excitations have the simple relationship given by,
Ebulk = √2Esurface -------------------------- [2313b]
On the other hand, the interpretation of the features of the low-loss regions from transition metals is more difficult because of some factors. In transition metals, both plasmon losses and interband transitions induce energy loss and the plamon losses generally do not occur at the energies theoretically predicted by free-electron model. Different from the case presented in Equation 2313b for free-electron metals, there is no simple relationship between the bulk and surface plasmon loss energies for a transition metal due to too much dependence on the band structure. Moreover, some electrons in certain d-bands may not be able to participate in collective plamon oscillations.
The contribution of bulk loss to single scattering distribution (SSD) is given by,
Ib(E,t) = t•[Ip(E) + Iint(E)+ICh(E)] ------------- [2313c]
where,
Ip -- The bulk plasmon-loss spectrum unit thickness.
Iint -- The interband transition spectrum unit thickness (the region of 0 to 10 eV).
ICh -- The Cherenkov radiation in unit thickness (the region of 0 to 10 eV).
An optical absorption method can directly provide the imaginary part of the dielectric function, ε2, associated with a single electron excitation of an interband transition, while EELS cannot directly give ε2. Therefore, based on the discussion in page4360, the real (ε1) and the imaginary (ε2) parts of the dielectric function can be extracted by a Kramers-Kronig analysis.
[1] K.S. Katti, M. Qian, F. Dogan, M. Sarikaya, J. Am. Ceram. Soc. 85 (2002)
2236–2243.
[2] K. van Benthem, C. Elsasser, R.H. French, J. Appl. Phys. 90 (2001) 6156–6164.
[3] S. Schamm, G. Zanchi, Ultramicroscopy 88 (2001) 211–217.
[4] J. Zhang, A. Visinoiu, F. Heyroth, F. Syrowatka, M. Alexe, D. Hesse, H.S. Leipner,
Phys. Rev. B 71 (2005) 064108.
|
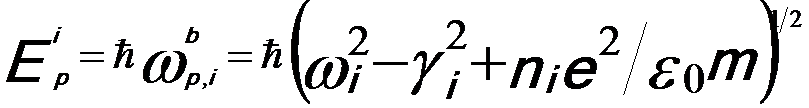 ------------------------- [2313a]
------------------------- [2313a]