=================================================================================
The purpose of the Ewald sphere is to determine which lattice planes will result in a reflection spot for the wavelength of an incident beam. The plane wave of the incident beam has a wave vector ki and the plane wave of the reflected beam has a wave vector kr. The difference between the wave-vectors of the reflected and incident waves can be given by scattering vector,
Δk = kr - ki ------------------------------ [2678a]
ki and kr have the same length, forming a sphere as shown in Figure 2678a. This sphere is called Ewald sphere.
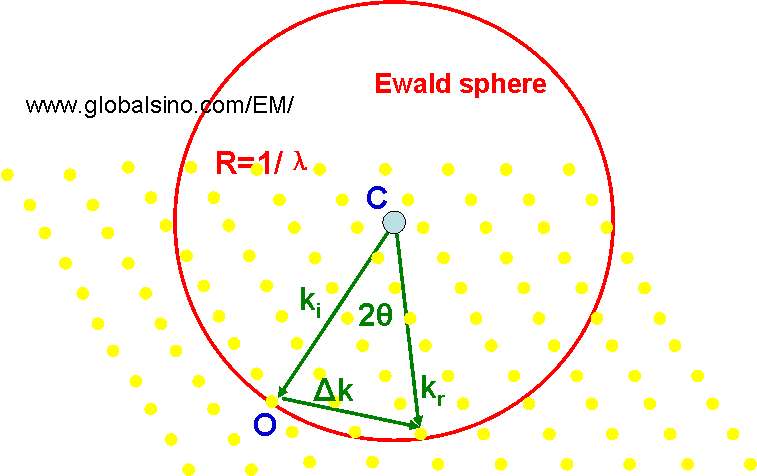
Figure 2678a. Schematic illustration of Ewald sphere construction.
In order to describe the Laue's diffraction conditions, we use a simple example which has a simple lattice with no basis,
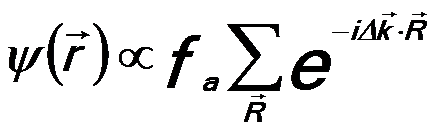 --------------------------------- [2678b] --------------------------------- [2678b]
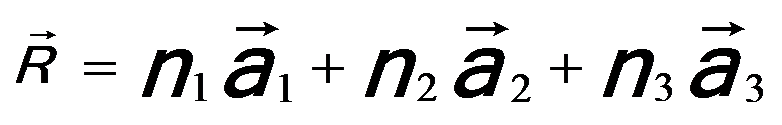 --------------------------------- [2678c] --------------------------------- [2678c]
Then, the lattice-sum can be separated as,
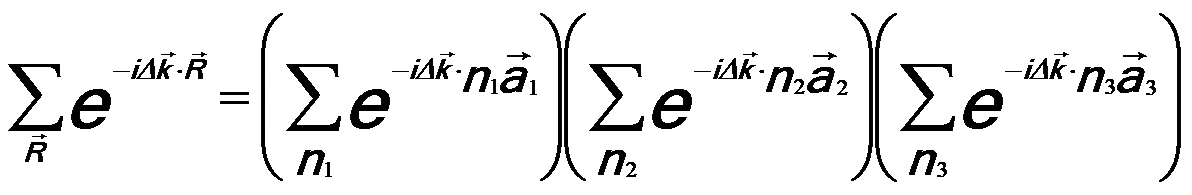 ----- [2678d] ----- [2678d]
When
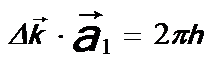 , --------------------------------- [2678e.a] , --------------------------------- [2678e.a]
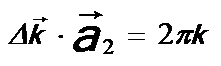 , --------------------------------- [2678e.b] , --------------------------------- [2678e.b]
and 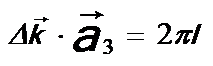 --------------------------------- [2678e.c] --------------------------------- [2678e.c]
then we have,
 --------------------------------- [2678f.a] --------------------------------- [2678f.a]
or 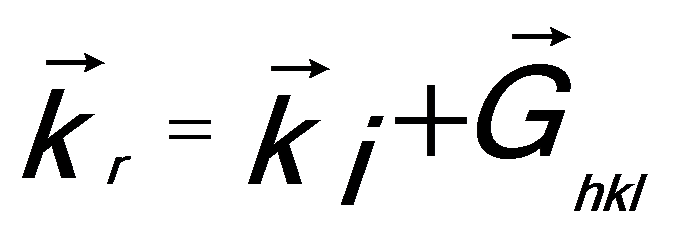 --------------------------------- [2678f.b] --------------------------------- [2678f.b]
Δk is given in Figure 2678a. The case given by Equations 2678f is called Laue‘s diffraction condition. Then, we can further have,
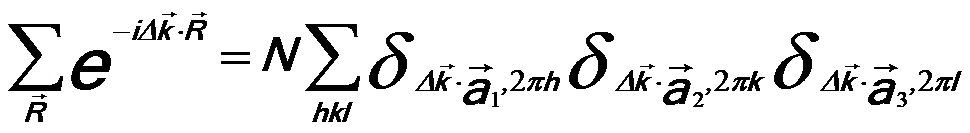 ---------- [2678g.a] ---------- [2678g.a]
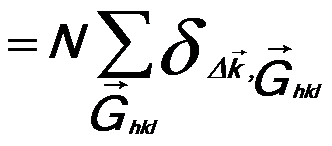 --------------------------------- [2678g.b] --------------------------------- [2678g.b]
where,
N -- The number of atoms
in the crystal.
From Equations 2678f, we can have,
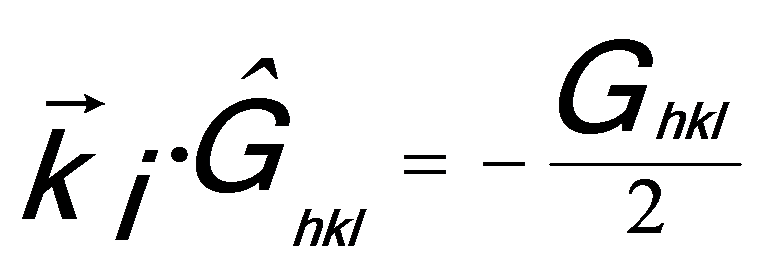 --------------------------------- [2678h] --------------------------------- [2678h]
At higher angles the Laue condition is no longer satisfied so that the ZOLZ intensity decreases to zero. However, when the Ewald sphere intercepts the HOLZ planes of reciprocal lattice this diffraction intensity returns.
|

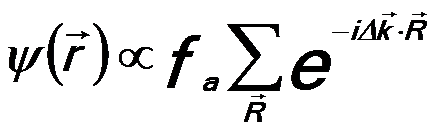 --------------------------------- [2678b]
--------------------------------- [2678b] 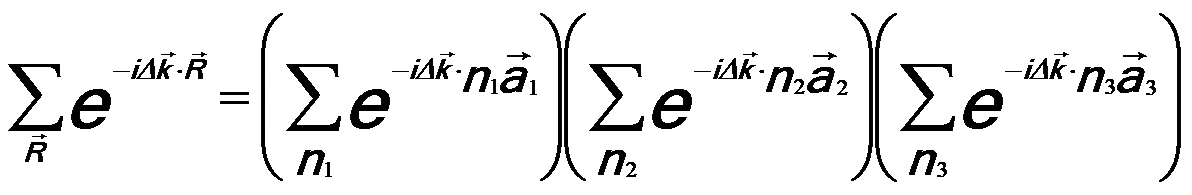 ----- [2678d]
----- [2678d] 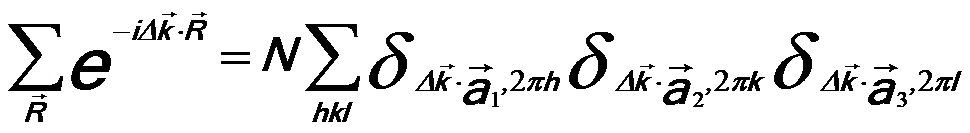 ---------- [2678g.a]
---------- [2678g.a] 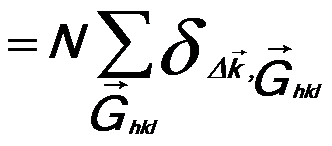 --------------------------------- [2678g.b]
--------------------------------- [2678g.b] 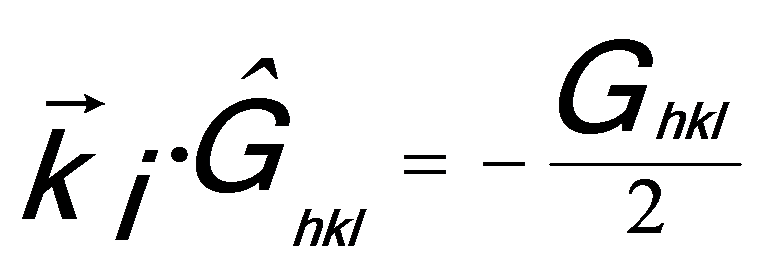 --------------------------------- [2678h]
--------------------------------- [2678h]