=================================================================================
Higher Order Laue Zones (HOLZs) in electron diffraction patterns are defined by the interception of the Ewald sphere with the allowed HOLZ relrods in the reciprocal lattice. Each of the HOLZs can be described by the equation given by,
hu + kv + lw = N ---------------------------------- [4783a]
where,
N -- An integer, called the order of the Laue zone.
[uvw] -- The direction of the incident electron beam.
hkl -- The coordinates of an allowed reflection in the Nth order Laue zone.
Therefore, HOLZ depends on the interplanar spacing in the crystal, the electron wavelength (i.e., the kV), L and any off-axis lens distortion. Ideal HOLZs are concentric at zero tilt, but increase their radius while moving off center to the upper left as the specimen is tilted. As examples, Figure 4783 shows FOLZ (First Order Laue Zones) and SOLZ (Second Order Laue Zones).
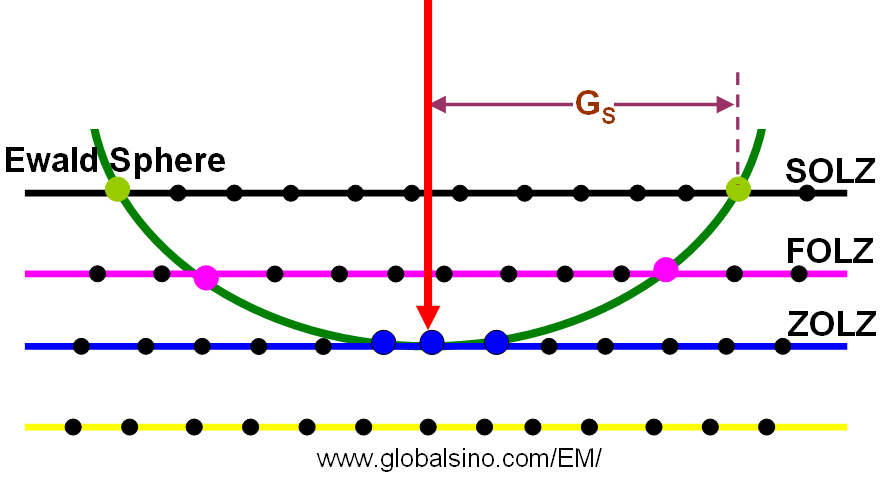
Figure 4783. Schematic of ZOLZ, FOLZ, and SOLZ.
The projected radius, Gn (nm-1 or Å-1), of a HOLZ ring can be given,
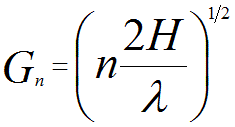 ----------------------------- [4783b] ----------------------------- [4783b]
where,
λ -- The electron wavelength.
H -- The spacing of the reciprocal lattice planes parallel to the electron beam.
n -- The order of the Laue zone
In diffraction observation, it is easier to observe smaller rings with any specific camera length L. Therefore, we normally tilt the TEM sample to a low symmetry zone axis in order to obtain a smaller H since this induces a smaller HOLZ ring than for a high symmetry zone axis.
We can convert reciprocal space H (nm-1) into real space 1/H (nm), and then Equation 4783b can be re-writen by,
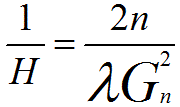 --------------------------------- [4783c] , --------------------------------- [4783c] ,
Then, we have,
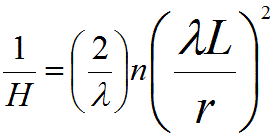 ----------------------------- [4783d] ----------------------------- [4783d]
where,
r -- The radius measured from the HOLZ ring in real space (mm).
λL -- The
camera constant (nm mm).
The projected radius can be measured from the recorded electron diffraction pattern if the HOLZ ring appears. Note that if the HOLZ ring is split, we always use the innermost ring for Gn. If we are measuring the rings at large scattering angles (e.g. ≥10°), then we need to use known standard samples to correct the distortion in reciprocal space. At such high angles, the electrons travel close to the polepiece and thus the lens imperfection causes the diffraction distortion. However, aberration correction, e.g. Cs correction, can minimize such distortion.
Note that to experimentally observe HOLZ reflections, the TEM specimen should normally be carefully tilted along mirrors until HOLZ areas appear on the pattern and long exposure time is normally needed since such reflections are often far away from the center of the screen and are weak.
At higher angles the Laue condition is no longer satisfied so that the ZOLZ intensity decreases to zero. However, when the Ewald sphere intercepts the HOLZ planes of reciprocal lattice this diffraction intensity returns. Note that practically we rarely find higher order reflections because the Ewald sphere intercepts the HOLZ at large scattering angles. On the other hand, the symmetry of the diffraction pattern from the ZOLZ is normally repeated in the HOLZ patterns.
The Precession electron diffraction (PED) patterns not only display more diffraction spots in the zero-order Laue zone (ZOLZ) than SAED ( selected-area electron diffraction) and NBED (nanobeam electron diffraction) but also show some diffraction spots in the high-order Laue zones (HOLZ) which normally do not show in SAED and NBED patterns. PED also can show more diffraction spots than the conventional diffraction techniques.
On the other hand, HOLZ lines are also formed by electron diffraction from the lattice planes of large reciprocal lattice vectors in the upper Laue zones. CBED patterns present the deficiency lines in the zero-order disc, which result from excitation of reflections in higher order Laue zones (HOLZ) and are called HOLZ lines. The positions of the HOLZ lines are related to the symmetry and lattice parameters of the crystal. They are changed in the direction of the applied stress if the material is stressed and those changes induce a change in the Bragg condition and thus a shift of the HOLZ lines. By analyzing their positions in combination with a reference CBED patern, a quantitative analysis of the three-dimensional (3-D) strain state of the crystal can be performed because the HOLZ lines are very sensitive to a small lattice strain. However, it is important to note that HOLZ reflections are sensitive to the changes of lattice parameters associated with the direction perpendicular to the electron incidence, but they are insensitive to the changes of lattice parameters associated with the electron incidence.
Note that it becomes difficult to observe the diffraction spots with high H K L values and the HOLZ rings at low or intermediate voltages since
the radius of the Ewald sphere increases with decreasing
electron wavelength λ.
|