Indexing of Trigonal and Hexagonal Systems - Practical Electron Microscopy and Database - - An Online Book - |
||||||||
| Microanalysis | EM Book https://www.globalsino.com/EM/ | ||||||||
| This book (Practical Electron Microscopy and Database) is a reference for TEM and SEM students, operators, engineers, technicians, managers, and researchers. | ||||||||
| ================================================================================= | ||||||||
For hexagonal lattices, there are normally three choices of unit cell as shown in Figure 3091a: Figure 3091a. Hexagonal net of the hexagonal P lattice: (a) Primitive hexagonal unit cell with six prism faces indexed {hkl}, (a) Hexagonal (four-index) unit cell with six prism faces indexed {hkil} and (c) Orthohexagonal unit cell. The z-axis points out of the plane of the page. The three-axis notation in Figure 3091a (a) can be converted to the four-axis notation in Figure 3091a (b) with the equations below: For instance, Similarly, the converting of hexagonal zone axes between Miller notation [U V W] and Miller-Bravais notation [u v t w] can be given by: For your convenience, the four-axis notations can be converted to the three-axis notations with the excel file, vice versa. Figure 3091b shows different crystal planes in hexagonal and trigonal crystal structures with four-index. The a-planes are given by the {11-20} facets, the c-planes by the {0002} facets, the m-planes by the {1-100} facets, and the r-planes by the {1-102} facets of the hexagonal unit cell. Figure 3091b. Different planes in the hexagonal and trigonal crystal lattices.
Now, we can figure out the Miller-Bravais notation for vector A in Figure 3091c: Figure 3091c. Example of extractions of Miller-Bravais notations. For hexagonal structures, the lattice spacing (d-spacing) can be given by, (You can download the excel file for your own calculations)
|
||||||||
| ================================================================================= | ||||||||
| The book author (Yougui Liao) welcomes your comments, suggestions, and corrections, please click here for submission. If you let book author know once you have cited this book, the brief information of your publication will appear on the “Times Cited” page. | ||||||||
|
|
||||||||
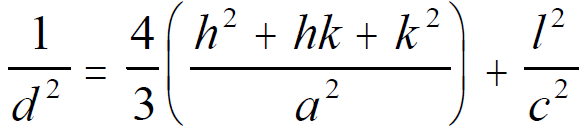 --------------------------------- [3091p]
--------------------------------- [3091p]