=================================================================================
If all of the atoms in a crystal are the same size, the maximum number of atoms that are coordinated around any individual is 12 (also called 12-fold coordination) in which there are two ways that atoms can be packed. For a single layer of atoms with an equal size, there are two kinds of voids between the atoms as shown in Figure 3550a (a):
i) B voids with triangles pointing up.
ii) C voids with the triangles pointing down.
Assuming a hard sphere model, atomic packing factor is defined as the ratio of atomic sphere volume to unit cell volume, which is 74% for both FCC and HCP and 68% for BCC. In general, ~90% elemental metals crystallize into three crystal structures which are BCC, FCC, and HCP.
As shown in Figure 3550a (b), if the second layer of atoms is added and its atoms occupy the space above the B voids followed by the third layer above the A atoms, this will result in hexagonal closest packing (HCP) with a stacking sequence of AB AB AB ....etc and with the c-axis perpendicular to the AB AB layers.
Figure 3550a. Formation of hexagonal closest packing (HCP): (a) Single layer of atoms, and (b) Formed HCP structure.
Close-packing of equal spheres (e.g. the same atoms in a crystal) can form the trigonal, hexagonal or cubic crystal systems. The structure belongs to the trigonal system if the structure has the minimum symmetry, while it belongs to the hexagonal system if it has a 63 axis of symmetry.
Table 3550a and Figure 3550b show the hexagonal crystal systems and the schematic illustrations of the hexagonal lattices, respectively. As indicated in Table 3550a, the structures belonging to the trigonal system can have either a rhombohedral or hexagonal lattice. The rhombohedral lattice are stacked in ABCABC...sequence, while the hexagonal lattice are stacked in AAA...sequence. Both the hexagonal (with 6-fold symmetry) and the trigonal (with 3-fold symmetry) systems require a hexagonal axial system.
Table 3550a. Hexagonal crystal systems.
Crystal
family |
Crystal
system |
Required
symmetries
of point group |
Point
group |
Space
group |
Bravais
lattices |
Lattice
system |
| Hexagonal |
Trigonal |
1 three-fold axis of rotation |
5 |
7 |
1 |
Rhombohedral |
| 18 |
1 |
Hexagonal |
| Hexagonal |
1 six-fold axis of rotation |
7 |
27 |
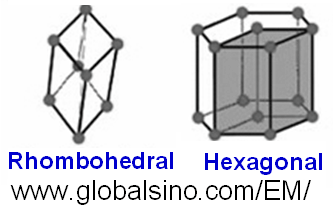
Figure 3550b. Schematic illustrations of the Bravais lattices of hexagonal crystals.
Table 3550b. Relationship between Laue classes and point groups.
System |
Essential symmetry |
|
|
|
| |
None |
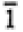 |
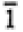 |
1, -1 |
| |
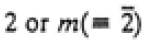 |
2/m |
2/m |
2, m, 2/m |
| |
222 or 2mm
|
mmm
|
mmm |
222, mm2, mmm |
| |
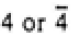 |
4/mmm
|
4/m
|
4, -4, 4/m |
| 4/mmm |
422, -42m, 4mm, 4/mmm |
|
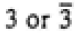 |
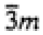 |
3 |
3, -3 |
| -3m1 |
321, 3m1, -3m1 |
| -31m |
312, 31m, -31m |
Hexagonal |
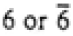 |
6/mmm
|
6/m |
6, -6, 6/m |
| 6/mmm |
622, -62m, 6mm, 6/mmm |
|
23 |
m3m
|
m-3 |
23, m-3 |
| m-3m |
432, -43m, m-3m |
For an ideal HCP structure, the c/a ratio is 1.63299. The volume of an unit cell in a hexagonal crystal is given by,
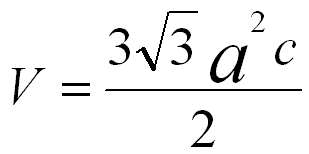 ------------------------------------ [3550] ------------------------------------ [3550]
According to Radius Ratio Rule, the limiting cation-to-anion radius ratios for HCP ionic lattices can be obtained as shown in Table 3550c.
Table 3550c. Cation-to-anion radius ratios (r+/r-) for coordination number (CN) 12.
|
CN |
Crystal type |
Material examples and their r+/r- |
1.0 |
12 |
Hexagonal or cubic
closest packing |
Metals |
For instance, at room temperature and ambient pressure, Ti (titanium) has a hexagonal close-packed structure (called α-phase) with the lattice constants listed in Table 1721a. Its unit cell has two atoms at (1/3, 2/3, 1/4) and (2/3, 1/3, 3/4) and the space group number is 194 (P63/mmc). At room temperature and high pressure, it changes to the ω-phase [1,2] with the lattice constants listed in Table 1721b. Its unit cell has three atoms at (0, 0, 0), (1/3, 2/3, 1/2), (2/3, 1/3, 1/2) and the space group is P6/mmm. The α → ω transition in Titanium is a typical example of martensitic transformation.
Table 3550d. Other characteristics of hexagonal structures.
Contents |
Page |
| Angles in unit cells |
page3555 |
| Volume of unit cells |
page3033 |
| Close packed planes and directions |
page3029 |
| Atomic packing factor |
page3030 |
| Number of lattice points (atoms) per unit cell |
page3032 |
| Coordination number of atoms |
page3031 |
| Relationship between three-dimensional crystal families, crystal systems, space group, point group, lattice systems and symmetries |
page4549 |
| Lattice point (or called Motif or basis) |
page3076 |
| Tables of Burgers vectors of dislocations and g·b |
page1995 |
| Bravais lattices |
page4546 |
| Dominating slip planes, slip directions and stable Burgers vector for common crystal structures |
page3557 |
[1] Jamieson J.C., Science, 1963, 140, 72; doi:10.1126/science.140.3562.72.
[2] Sikka S.K., Vohra Y.K., Chidaraman R., Prog. Mater. Sci., 1982, 27, 245.
|
