=================================================================================
Table 3551a and Figure 3551a show the tetragonal crystal systems and the schematic illustrations of the tetragonal lattices, respectively. Furthermore, Table 3551c shows the cell edges and angles of tetragonal crystals.
Table 3551a. Tetragonal crystal systems.
Crystal
family |
Crystal
system |
Required
symmetries
of point group |
Point
group |
Space
group |
Bravais
lattices |
Lattice
system |
Tetragonal |
1 four-fold axis of rotation |
7 |
68 |
2 |
Tetragonal |
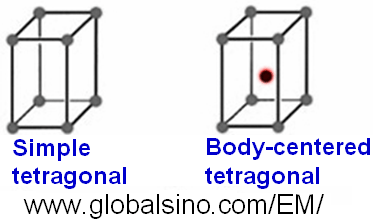
Figure 3551a. Schematic illustrations of the Bravais
lattices of tetragonal crystals.
Table 3551b. Relationship between Laue classes and point groups.
| System |
Essential symmetry |
Lattice symmetry |
Laue class (Diffraction symmetry) |
Point Groups (Hermann–Mauguin notation) |
| Triclinic |
None |
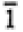 |
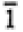 |
1, -1 |
| Monoclinic |
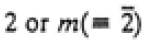 |
2/m |
2/m |
2, m, 2/m |
| Orthorhombic |
222 or 2mm
|
mmm
|
mmm |
222, mm2, mmm |
| Tetragonal |
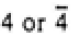 |
4/mmm
|
4/m
|
4, -4, 4/m |
| 4/mmm |
422, -42m, 4mm, 4/mmm |
| Trigonal |
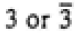 |
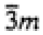 |
3 |
3, -3 |
| -3m1 |
321, 3m1, -3m1 |
| -31m |
312, 31m, -31m |
| Hexagonal |
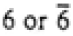 |
6/mmm
|
6/m |
6, -6, 6/m |
| 6/mmm |
622, -62m, 6mm, 6/mmm |
| Cubic |
23 |
m3m
|
m-3 |
23, m-3 |
| m-3m |
432, -43m, m-3m |
For tetragonal structures, the lattice spacing (d-spacing) can be given by, (You can download the excel file for your own calculations)
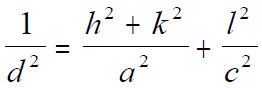 --------------------------------- [3551] --------------------------------- [3551]
where,
a and c -- The lattice constants.
h, k, and l -- The Miller indices.
As shown in Figure 3551b, in a cubic transition-metal (TM) oxide crystal, the divalent TM ion is in a site that has octahedral Oh symmetry and the d-levels split into threefold degenerate (lower energy) t2g states and twofold degenerate (higher energy) eg states that can accommodate six and four electrons, respectively (including spin states). The tetragonal symmetry splits the levels further. The t2g states split into a singlet, dxy, and a doublet dxz and dyz. The eg states split into d3z2-r2 and dx2-y2 levels.
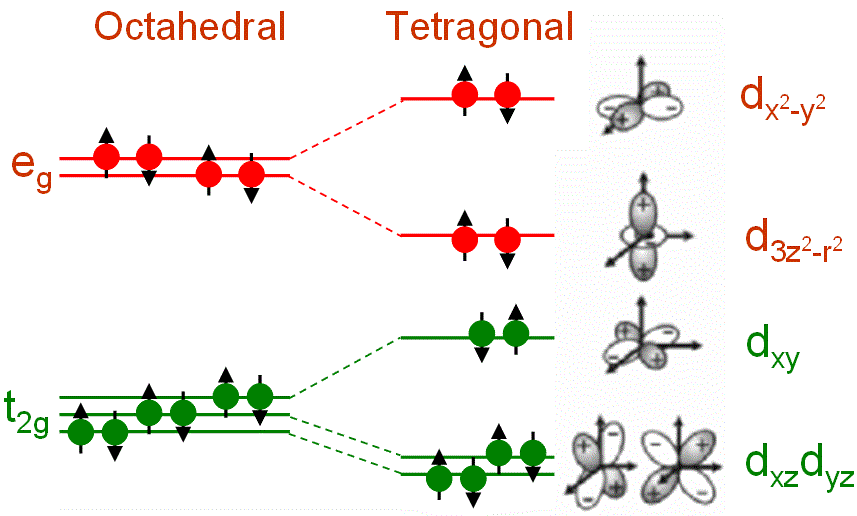
Figure 3551b. Ligand field splitting of d orbitals in an octahedral ligand field.
In some TM (transition metal) cases, the filling of orbitals with electrons may affect the local structure and thus induce geometrical distortion around the TM ion. The Jahn–Teller effect, also called Jahn–Teller distortion, describes this type of distortions. A typical Jahn-Teller ion is Mn3+ as shown in Figure 3551c. The ion in the high-spin configuration contains a single electron in the upper eg state when it is placed in an octahedral LF (ligand field). A tetragonal distortion can lower the energy of the system. The lowering in total energy is due to the lowering of one of the eg orbitals by lengthening the bond along the z axis. Note that the overall energy of the system is not further lowered by splitting the t2g state because the center of gravity is retained.
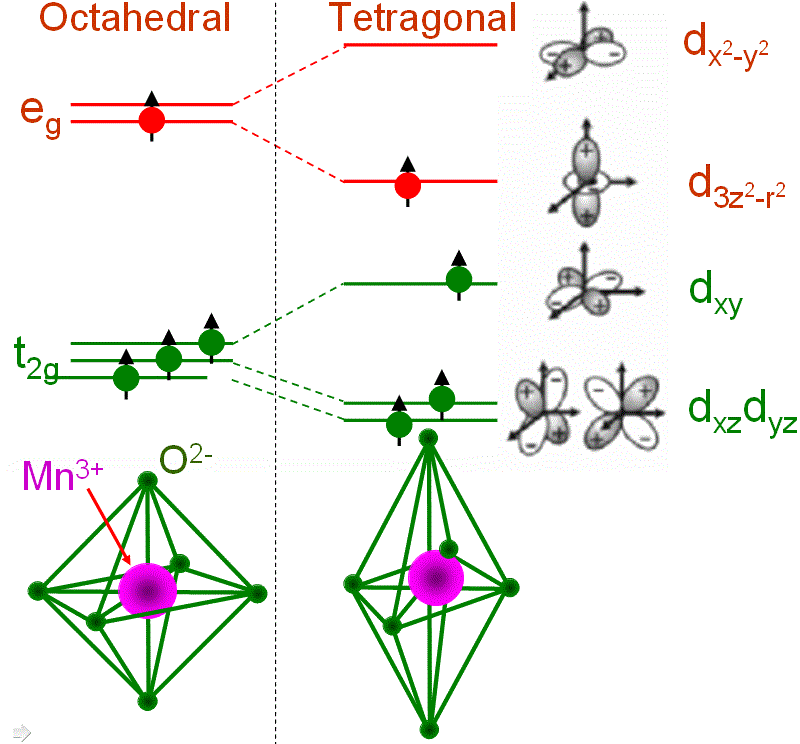
Figure 3551c. John-Teller effect for Mn3+ (3d4).
Table 3551c. Other characteristics of tetragonal structures.
Contents |
Page |
| Angles in unit cells |
page3555 |
| Volume of unit cells |
page3033 |
| Bravais lattices |
page4546 |
| Relationship between three-dimensional crystal families, crystal systems, space group, point group, lattice systems and symmetries |
page4549 |
|

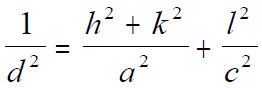 --------------------------------- [3551]
--------------------------------- [3551]