Introduction of unit cells in crystals and lattice parameters (constants/spacing)

Introduction of Unit Cells in Crystals
& Lattice Parameters (Constants/Spacing)
- Practical Electron Microscopy and Database -
- An Online Book -

Microanalysis | EM Book https://www.globalsino.com/EM/

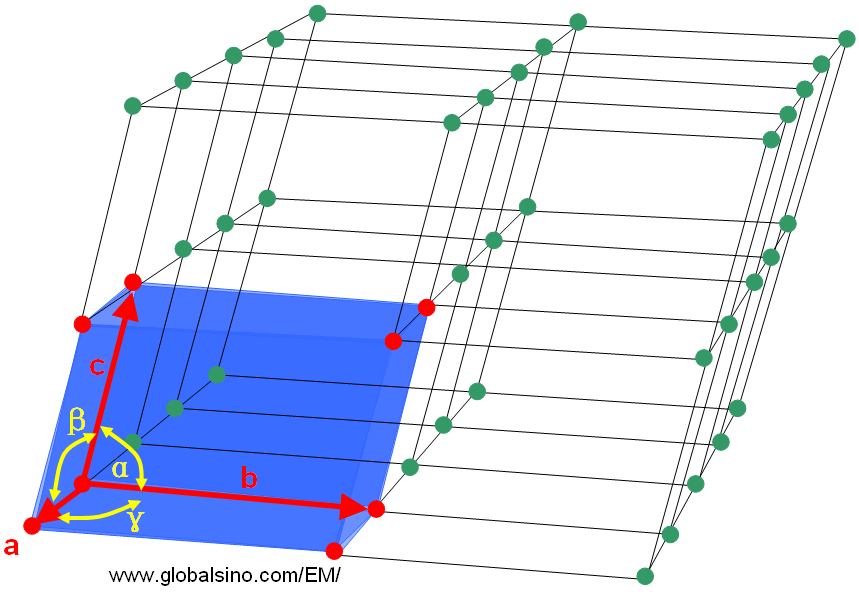
The smallest repeating three-dimensional (3-D) volume of the lattice is called a unit cell. Abbé Haüy [1] showed that the periodic repetition of identical parallelepipeds (molécules intégrantes, now known as unit cells) could be used to explain the external shape of crystals in 1784.

As shown in Figure 3555a, the unit cell is characterized by three lattice parameters (constants) a, b, and c (the lengths of the basis vectors indicated by the red arrows) and by the three angles α, β, and γ (in yellow) which separate these vectors from one another. The angle α is the angle between the basis vectors b and c, β between a and c, and γ between a and b. The lattice parameters of organic or inorganic structures are of the range of 3 to 40 Å and for protein structures they can be up to 100 Å or more.

Part of a lattice with a unit cell indicated

Figure 3555a. Part of a lattice with a unit cell indicated by the blue box and red dots.

A unit cell retains all the characteristics of a lattice and has a specific shape. Each unit cell is based on:
        i) The highest symmetry
        ii) Consistency with past convention
        iii) Minimized unit cell volume
        iv) Satisfaction of minimal symmetry requirements.

Bravais lattices can be classified in terms of the number of lattice points in the unit cell. Table 3555 also shows the seven crystal systems and the restrictions on their cell dimensions (cell edges and cell angles).

Table 3555. The seven crystal systems (families) and the restrictions on their cell dimensions.

Crystal family	Cell edges (parameters)	Cell angles
Triclinic	a ≠ b ≠ c	α ≠ β ≠ γ (All angles are different and none equals 90°.)
Monoclinic	a ≠ b ≠ c	α = γ = 90° (Two angles equal 90°, one angle (β) is not equal to 90°)
Orthorhombic	a ≠ b ≠ c	α = β = γ = 90° (All angles equal 90°)
Rhombohedral	a = b = c	α = β = γ (All angles are equal and none equals 90°)
Tetragonal	a = b ≠ c	α = β = γ = 90° (All angles equal 90°)
Trigonal, hexagonal	a = b ≠ c	α = β = 90°, γ = 120° (Two angles equal 90°, one angle equals 120°)
Cubic	a = b = c	α = β = γ = 90° (All angles equal 90°)

The number of the lattice points per unit cell in 2-D lattices can be given by,
---------------------------- [3555a]
where,
N_Interior and N_Corner - The numbers of the lattice points inside the unit cell and at the corners, respectively, as shown in Figure 3555b.

Lattice points inside the unit cell and at the corners in 2-D lattices

Figure 3555b. Lattice points inside the unit cell and at the corners in 2-D lattices.

On the other hand, the number of the lattice points per unit cell in 3-D lattices can be given by,
---------------------------- [3555b]
where,
N_Face - The number of the lattice points at the faces as shown in Figure 3555c.

Lattice points inside the unit cell and at the corners in 2-D lattices

Figure 3555c. Lattice points inside the unit cell and at the corners in 3-D lattices.

[1] R.J. Haüy, Essai d'une théorie sur la structure des cristaux, (1784).

;