=================================================================================
The unique arrangements of lattice points are so-called Bravais lattice, named after Auguste Bravais. Space groups represent the ways that the macroscopic and microscopic symmetry elements (operations) can be self-consistently arranged in space. In two-dimensional (2-D) lattices, there are five distinct Bravais lattices.
In three-dimensional (3-D) lattices, there are totally 230 space groups. The space groups add the centering information and microscopic elements to the point groups. Figure 4546 schematically shows the relationship between the 7 crystal systems, 14 Bravais Lattices, 32 point groups, and 230 space groups.
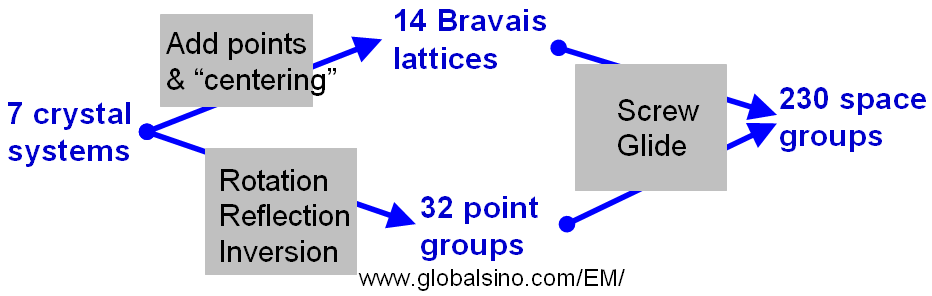
Figure 4546. The relationship between the 7 crystal systems,
14 Bravais Lattices, 32 point groups, and 230 space groups.
Table 4546 also lists the relation between three-dimensional crystal families, crystal systems, and lattice systems. The lattices are classified in 6 crystal families and are symbolized by 6 lower case letters a, m, o, t, h, and c. The classifications of crystal families and crystal systems are the same except the hexagonal family. The first letter of the Bravais lattice symbols is denoted with the symbol of the crystal family, and the second letter is a capital letter (P, S, I, F, R) that represents the Bravais lattice centering. The symbol S denotes an one-face centered lattice (See page3021 for detailed descriptions on the other letters).
Table 4546. The relation between three-dimensional crystal families, crystal systems, and lattice systems.
Crystal
system |
Crystal
family |
Required symmetries of point group |
Point
group |
Space
group |
Bravais
lattices |
Pearson symbol |
Coordinate description |
| |
Symbol |
No. |
Symbol |
Name |
| Triclinic (anorthic) |
a |
None |
2 |
2 |
1 |
aP |
Primitive triclinic (P) |
aP* |
|
Monoclinic
|
m |
1 two-fold axis of rotation, rotary inversion axis along b, or 1 mirror plane |
3
|
13
|
2
|
mP |
Simple monoclinic (P) |
mP* |
a≠b≠c,
α=γ= 90°, β≠90° |
| mS (mA, mB, mC) |
Base-face centered monoclinic (C) |
mS* |
Orthorhombic |
o |
Three mutually perpendicular 2-fold axes of rotation, rotatory-inversion axes along a, b, and c, or one 2-fold axis of rotation and two mirror planes. |
3 |
59 |
4 |
oP |
Primitive orthorhombic (P) |
oP* |
a≠b≠c,
α=β=γ=90° |
| oF |
Face centered orthorhombic (C, F) |
oF* |
| oS (oA, oB, oC) |
Base-centered orthorhombic |
oS* |
| oI |
Body centered orthorhombic (I) |
oI* |
Tetragonal |
t |
A single 4-fold rotation or rotatory-inversion axis along c |
7 |
68 |
2 |
tP |
Primative tetragonal (P) |
tP* |
a=b≠c,
α=β=γ=90° |
| tI |
Body centered tetragonal (I) |
tI* |
| Trigonal |
Hexagonal |
h |
Identity or inversion in any direction. |
5 |
7 |
1 |
hR |
Trigonal (P) |
|
a≠b≠c,
α≠β≠γ≠90° |
| One 3-fold rotation axis along c |
18 |
1 |
Primative rhombohedral (P) |
hR* |
a=b=c,
α=β=γ≠90° |
| Hexagonal |
A single 6-fold rotation or rotatory-inversion axis along c |
7 |
27 |
1 |
hP |
Hexagonal (P) |
hP* |
a=b≠c,
α=β=90°, γ=120° |
Cubic
|
c |
Four 3-fold rotation axes along a+b+c, -a+b+c, a-b+c, -a-b+c. |
5 |
36 |
3 |
cP |
Primitive cubic (P) |
cP* |
a=b=c,
α=β=γ=90°
|
| cF |
Face centered cubic (F) |
cF* |
| cI |
Body centered cubic (I) |
cI* |
| Total: 7 |
6 |
|
|
32 |
230 |
14 |
|
|
|
|
| * = sum of multiplicities of all atom sites in the structure. |
Bravais lattices can be classified in terms of the number of lattice points in the unit cell. Figure 4546 shows the schematic illustrations of the Bravais Lattices. The array of points for each Bravais Lattice repeat periodically in three-dimensional space.
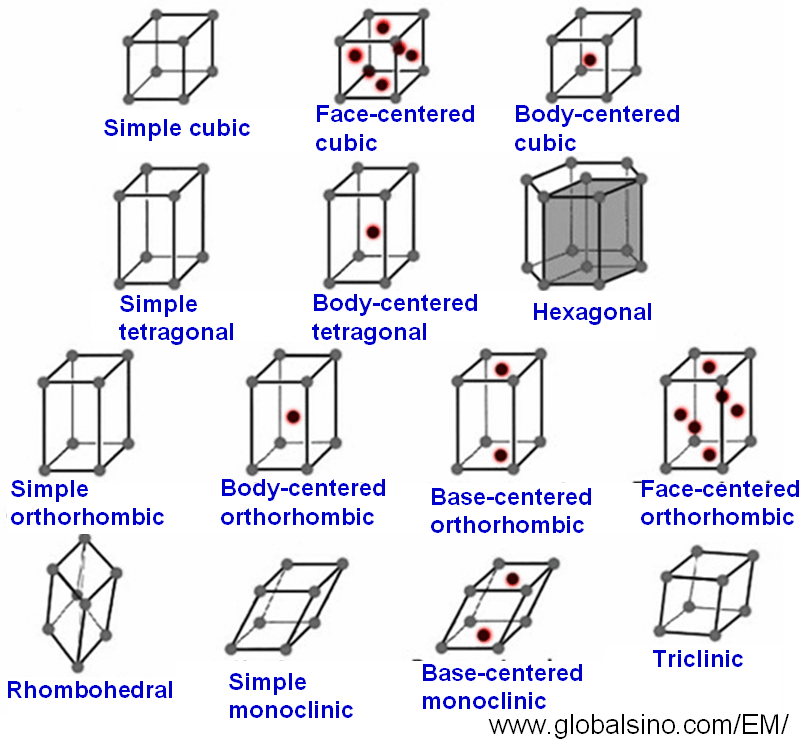
Figure 4546. Schematic illustrations of the Bravais Lattices.
Pearson symbol represents crystal system, type of Bravais lattice and number of atoms in an unit cell. For instance, a face-centered cubic (FCC) structure is a face-centered Bravais lattice having 4 atoms in the unit cell, and thus its Pearson symbol is cF4. In this notation, the crystal system is simplified by a = triclinic, m = monoclinic, o = orthorhombic, t = tetragonal, h = hexagonal and trigonal and c = cubic. The Bravais lattice is symbolized by P, S (for A, B and C), R, F and I.
|

