=================================================================================
Face-centered cubic (fcc) crystals are common among metals at low temperatures because the atoms pack well. Steels are body-centered cubic at low temperatures and face-centered cubic at high temperatures. For FCC and HCP systems, the coordination numbers are 12, while for BCC it’s 8. Assuming a hard sphere model, atomic packing factor is defined as the ratio of atomic sphere volume to unit cell volume, which is 74% for both FCC and HCP and 68% for BCC. In general, ~90% elemental metals crystallize into three crystal structures which are BCC, FCC, and HCP.
Table 2872a. Some normalized surface energies of low-index surfaces of fcc.
Solid
|
(100)
|
(110)
|
(111) |
(311) |
(531) |
(210) |
|
|
|
|
|
|
|
Table 2872b lists the characteristics of the three cubic Bravais lattices.
Table 2872b. The only three cubic Bravais lattices.
Lattice |
Number of
lattice points
per unit cell |
Number of
atoms
per unit cell |
Nearest distance
between lattice points |
Maximum packing |
Maximum packing condition |
Density (or fraction of packing, Vatom/Vcell) |
|
1 |
1 |
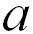 |
When the adjacent atoms touch each other along the edge
of the cube |
52.4% |
|
2 |
2 |
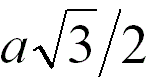 |
When the adjacent atoms touch each other along
the body diagonal of the cubic cell |
68.0% |
FCC |
4 |
4 |
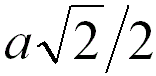 |
When the adjacent atoms touch each other along
the face diagonal of the cubic cell |
74.0% |
|
4 |
8 |
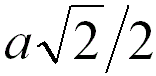 |
|
34 % |
For FCC and BCC structures, the lattice constants are given by, (For FCC, you can download the excel file for your own calculations)
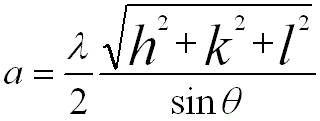 ----------------- [2872] ----------------- [2872]
Table 2872c. Other characteristics of FCC structures.
Contents |
Page |
| Close packed planes and directions |
page3029 |
| Atomic packing factor |
page3030 |
| Number of lattice points (atoms) per unit cell |
page3032 |
| Lattice point (or called Motif or basis) |
page3076 |
| Coordination number of atoms |
page3031 |
| Space groups |
Fm-3m (225), F4-3m (216), Fd-3m (227), Pm-3m (221) |
| d-spacing ratios of allowed Bragg reflections |
1, √3, √4, √8, √11, √12, √16, √19, √20, √24, √27, ... |
| Tables of Burgers vectors of dislocations and g·b |
page1995 |
| Dominating slip planes, slip directions and stable Burgers vector for common crystal structures |
page3557 |
| Digital Micrograph script to compute reflection angle |
Script link |
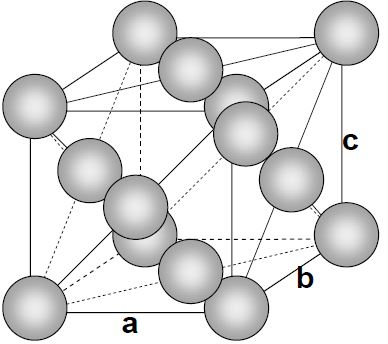
Figure 2872a. Atomic structure of FCC.
|