=================================================================================
Comparing with other crystal structures, body-centered cubic (bcc) packings of atoms tend to be most stable near the melting point of materials because the atoms have room to vibrate (important at high temperatures). Steels are body-centered cubic at low temperatures and face-centered cubic at high temperatures. For FCC and HCP systems, the coordination numbers are 12, while for BCC it’s 8. Assuming a hard sphere model, atomic packing factor is defined as the ratio of atomic sphere volume to unit cell volume, which is 74% for both FCC and HCP and 68% for BCC. In general, ~90% elemental metals crystallize into three crystal structures which are BCC, FCC, and HCP.
Figure 2873 shows the effects of structural symmetry on XRD patterns. These effects include the difference of the reflection numbers and the peak splitting for the tetragonal and orthorhombic structures, for instance, shown in the red dotted box.
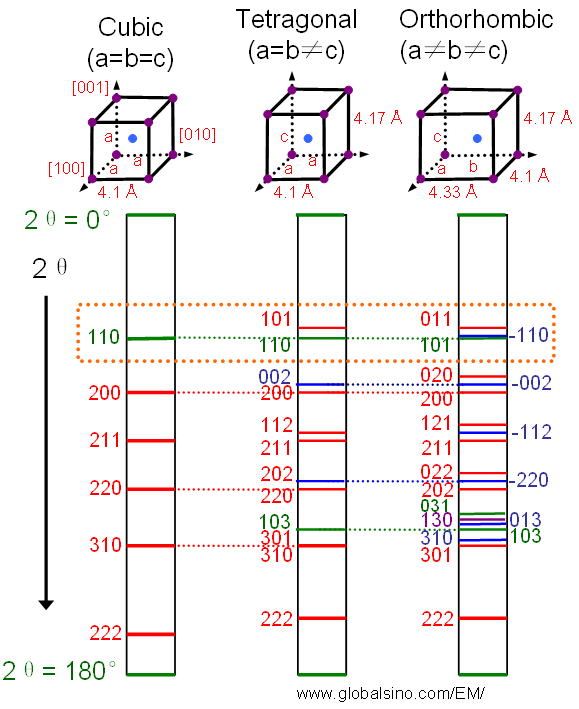
Figure 2873. The effects of structural symmetry on XRD patterns: (a) body-centered-cubic (bcc), (b) body-centered-tetragonal (bct), and (c) body-centered-orthorhombic (bco).
Table 2873a. Example of compounds with similar structures to BCC.
| |
BCC |
|
|
|
| Space group |
Im-3m |
P42/mnm |
Pm-3m |
Pn-3m |
| Compounds |
α-Fe, W, Nb, Ta, Na, K, Mo, V |
GeO2, SnO2, PbO2 |
CsI, CsBr, CsCl |
Pb2O, Ag2O |
Table 2873b. Some normalized surface energies of low-index surfaces of bcc.
Solid |
(100)
|
(110)
|
(111) |
(211) |
|
|
|
|
|
Table 2873c. Some symmetrical diffraction patterns of cubic crystals.
Zone axis |
[100] |
[110] |
[111] |
Symmetry |
Square |
Rectangular |
Hexagonal |
Aspect Ratio |
1:1 |
1: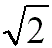 for BCC, SC (almost hexagonal for FCC) for BCC, SC (almost hexagonal for FCC) |
Equilateral |
Table 2873d lists the characteristics of the three cubic Bravais lattices.
Table 2873d. The only three cubic Bravais lattices.
Lattice |
Number of
lattice points
per unit cell |
Number of
atoms
per unit cell |
Nearest distance
between lattice points |
Maximum packing |
Maximum packing condition |
Density (or fraction of packing, Vatom/Vcell) |
|
1 |
1 |
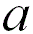 |
When the adjacent atoms touch each other along the edge
of the cube |
52.4% |
BCC |
2 |
2 |
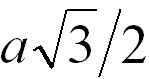 |
When the adjacent atoms touch each other along
the body diagonal of the cubic cell |
68.0% |
|
4 |
4 |
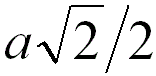 |
When the adjacent atoms touch each other along
the face diagonal of the cubic cell |
74.0% |
|
4 |
8 |
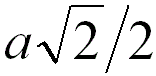 |
|
34 % |
For FCC and BCC structures, the lattice constants are given by, (For BCC, you can download the excel file for your own calculations)
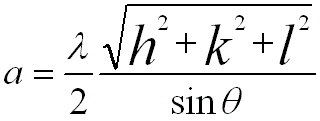 ----------------- [2873] ----------------- [2873]
Table 2873e. Other characteristics of BCC structures.
Contents |
Page |
| Close packed planes and directions |
page3029 |
| Atomic packing factor |
page3030 |
| Number of lattice points (atoms) per unit cell |
page3032 |
| Coordination number of atoms |
page3031 |
| Space groups |
Im-3m (229) |
| d-spacing ratios of allowed Bragg reflections |
1, √2, √4, √6, √8, √10, √12, √14, √16, √18, √20, ... |
| Tables of Burgers vectors of dislocations and g·b |
page1995 |
| Dominating slip planes, slip directions and stable Burgers vector for common crystal structures |
page3557 |
| Digital Micrograph script to compute reflection angle |
Script link |
|