=================================================================================
The virtual objective apertures (VOAs) in SEMs and STEMs limit the beam angles in a similar manner to real objective apertures. However, for the same beam convergence angle the VOA opening required is equal to the size of the equivalent real aperture divided by the demagnification of the objective.
In conventional EM system, the existence of spherical aberration requires the utility of very small apertures to maximize the spatial resolution, while the resolution will also be limited by diffraction if the apertures are too small. Scherzer suggested that the maximum aperture size (given by convergence semi-angle), α0, should be defined by limiting the phase error across the aperture to the values equal to or smaller than a quarter wavelength (i.e. |χ(α)| ≤ π/2) by balancing Δf against Cs.
According to the theory on the phase shift induced by defocus and spherical aberration, χ can be given by,
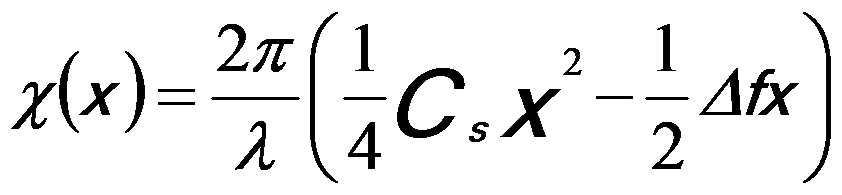 ------------------ [3591a] ------------------ [3591a]
Here, α2 (see page3731) is replaced by x. Therefore, we can obtain that the minimum χ(x) at,
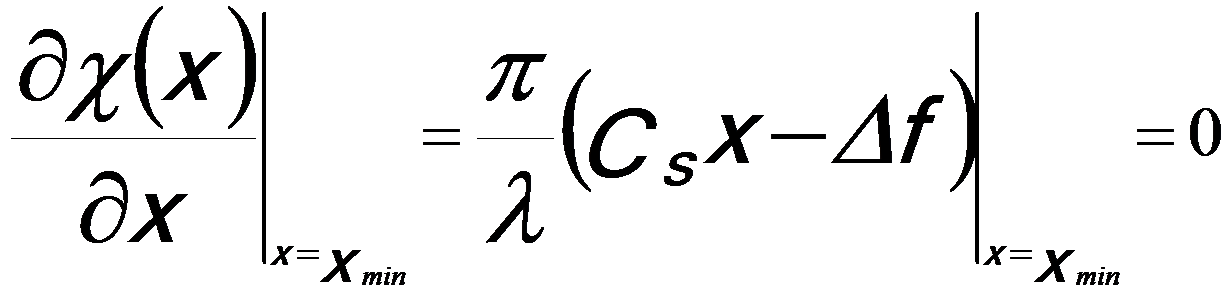 ------------------ [3591b] ------------------ [3591b]
So that,
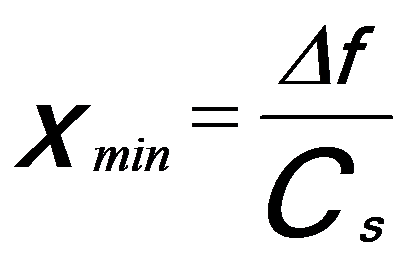 ------------------ [3591c] ------------------ [3591c]
Based on the assumption χ(xminimum) = - π/2 and Equations 3591a and 3591c, one can obtain the optimal defocus,
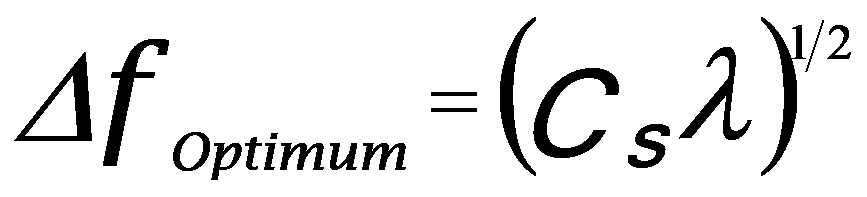 ------------------ [3591d] ------------------ [3591d]
The largest, optimized aperture size (i.e. the maximum convergence semi-angle, α0) is set to the point with χ (α ) = 0, so that based on Equation 3591a, one can obtain,
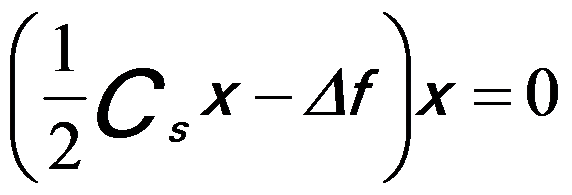 ------------------ [3591e] ------------------ [3591e]
For x ≠ 0, the optimum semi-angle of the electron beam, representing the compromise between the spherical aberration and aperture, is given by,
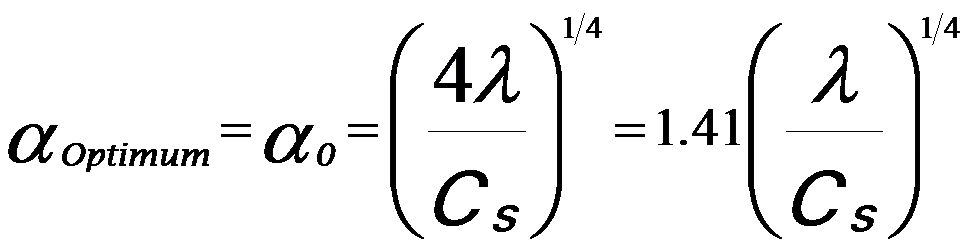 ------------------ [3591f] ------------------ [3591f]
where,
β -- The semi-angle of the electron beam;
Cs -- The spherical aberration coefficient;
λ -- The wavelength of the electrons in the beam.
Equation 3591f indicates that the optimum semi-angle affects the selection of the aperture size during SEM and STEM operations. This optimal aperture size given by Equation 3591f is smaller than the optimal objective aperture size for coherent imaging in TEM (αOptimum = 1.56 (λ/Cs)1/4), which is also known as the Scherzer aperture.
The optimal size of the objective aperture in STEMs was also evaluated by applying the point spread function to minimize the probe tails at the expense of increasing the central disc [1]. This optimal size is given by,
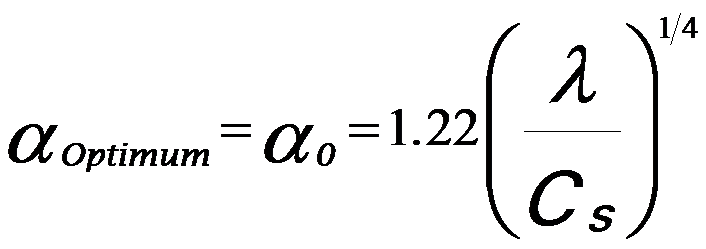 ------------------ [3591g] ------------------ [3591g]
Based on the circle of the least confusion related to spherical aberration, the spatial resolution can be given by,
d0 = 0.6 Cs1/4 λ3/4 -------------------------------- [3591h]
[1] E.J. Kirkland, Advanced Computing in
Electron Microscopy. 1998, NY: Plenum.
|
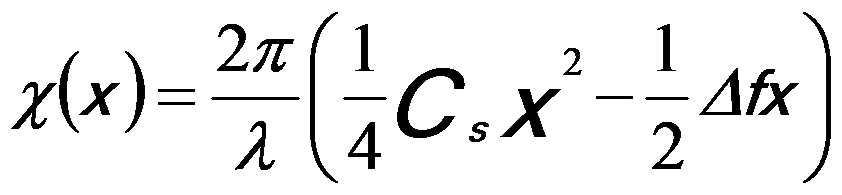 ------------------ [3591a]
------------------ [3591a] 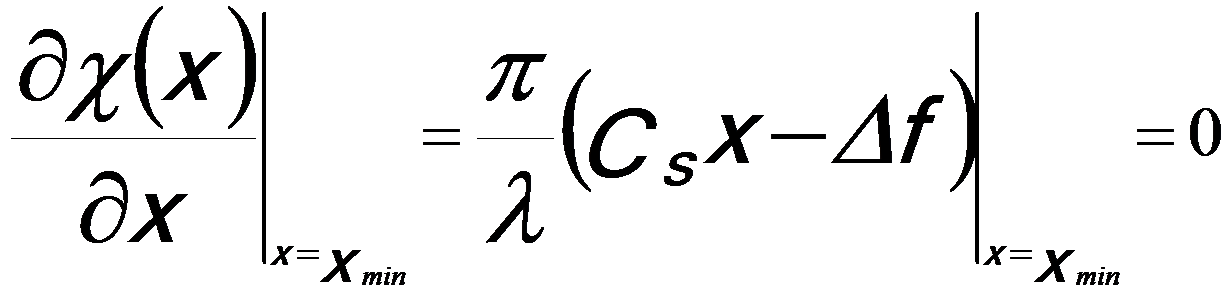 ------------------ [3591b]
------------------ [3591b] 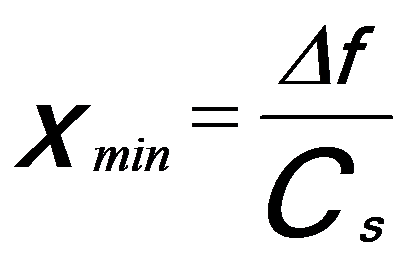 ------------------ [3591c]
------------------ [3591c] 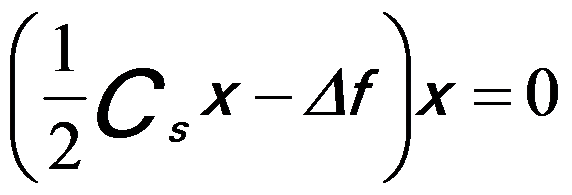 ------------------ [3591e]
------------------ [3591e] 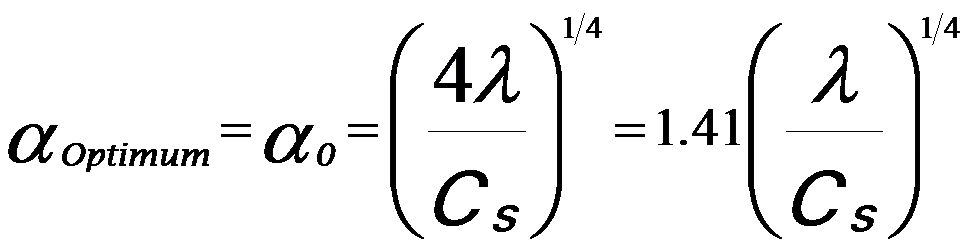 ------------------ [3591f]
------------------ [3591f] 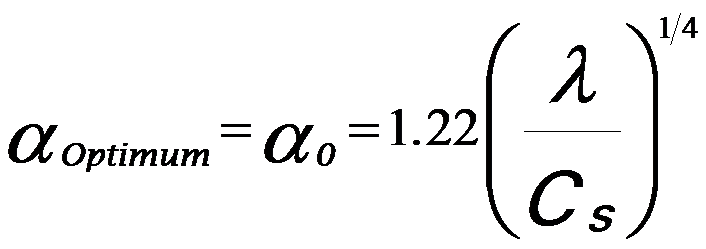 ------------------ [3591g]
------------------ [3591g]