This book (Practical Electron Microscopy and Database) is a reference for TEM and SEM students, operators, engineers, technicians, managers, and researchers.

=================================================================================

The main inelastic scattering mechanisms are:
         i) Phonon excitation (heat).
         ii) Plasmon excitation (valence electrons).
         iii) Single electron excitation (inner and outer shell scattering).
         iv) Direct radiation losses (Bremsstrahlung radiation due to deceleration of the electron beam in the Coulomb field of an atom).
         v) Excitation of conducting electrons leading to secondary electron emissions.

Except for the single-electron excitation, inelastic scattering of outer-shell electrons under high energy electron irradiation in EMs can involve many atoms in the specimen. Based on quantum theory, this excitation can be described in terms of the creation of a pseudoparticle (plasmon) at energy of E_p = ħω_p ( ħ is Planck’s constant and ω_p is the plasmon frequency). For most solids, E_p is in the energy range of 5–30 eV.

In physics, a plasmon is a quantum of plasma oscillation (also called plasma resonance) and in practice is a collective charge oscillation. These charges in EMs measurements are free electrons induced by the incident electron beam. Plasmon-like oscillations occur even in non-metallic materials where there are no obvious free electrons. The non-localized scattering events of plasma occur over a number of atomic sites, typically in the range of 100 nm.

The valence electrons in alkali metals act as free particles so that the collective form of excitation response (plasmon effect) detected by EELS is predominant (compared with single-electron excitation). In contrast, in rare gas solids, plasmon effects in EELS are weak or nonexistent. The other materials fall in between these plasmon excitation and single-electron excitation.

In electron microscope, due to change of energy electrons after inelastic scattering are incoherent, and plasmons are the primary way of inelastic electron scattering.

The EELS of the low-energy loss region less than 50 eV is particularly called valence electron energy loss spectroscopy (VEELS) and mainly reflects the excitation of valence band electrons, such as interband transition (single excitation) and plasmon excitation (collective excitation). VEELS can be applied to analyze, for instance, local electronic and optical properties of materials [1] in nanoscale with STEM [2–7]. The STEM-VEELS method provides various advantages over conventional optical spectroscopy, for instance, it can measure a wider energy (wavelength) range and local electronic and optical properties from a small volume in a nano-region. The difficulty of STEM-VEELS application is that it is hard to fit a zero-loss tail, to extract ELF (energy loss function) attributable to the large zero-loss tail and to interpret the collective excitation such as plasmon, etc.

Figure 4128a shows angular distribution of scattered electrons, with plasmon losses, as a function of scattering angle in EMs.

Figure 4128a. Plasmon losses.

Figure 4128b shows the schematic illustration of an energy-loss spectrum and the formation of the main energy-loss peaks (e.g. plasmon peak) related to the energy levels of electrons surrounding atom A and atom B in materials.

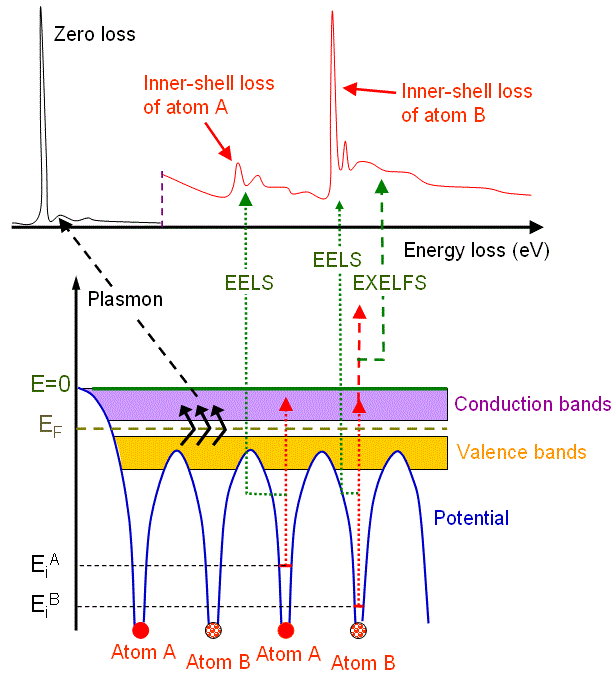
Figure 4128b. Schematic illustration of an energy-loss spectrum and the formation of three main energy-loss peaks.

Plasmon excitation requires much less energy, while ionization requires more energy and thus the ionization cross-sections are relatively small and the mean-free paths relatively large. Therefore, the intensity of ionization in the spectrum is smaller than the plasmon peak and becomes even smaller as the energy loss increases.

   
[1] R. F. Egerton, Electron Energy Loss Spectroscopy in the Electron Microscope (Plenum, New York, 1996).
[2] N. Ikarashi, K. Manabe, J. Appl. Phys. 94 (2003) 480–486.
[3] N. Ikarashi, K. Manabe, Appl. Phys. Lett. 80 (2002) 4127–4129.
[4] N. Ikarashi, M. Murata, K. Masuzaki, T. Tastumi, Appl. Phys. Lett. 84 (2002) 3672–3674.
[5] D.W. McComb, Phys. Rev. B 54 (1996) 7094–7102.
[6] L. Ryen, X.Wang, U. Helmersson, E. Olsson, J. Appl. Phys. 85 (1999) 2828–2834.
[7] P.E. Batson, K.L. Kavanagh, J.M. Woodall, J.W. Mayer, Phys. Rev. Lett. 57 (1986) 2729–2732.