=================================================================================
Inelastic interactions of electrons with solids are very important for many measurement
techniques such as energy loss spectroscopy, low energy electron diffraction,
photoemission spectroscopy and time-resolved two-photon photoemission. The mean free path of an electron (average speed times the scattering time) is the
average distance an electron travels between two consecutive scattering events as shown in Figure 4476a.
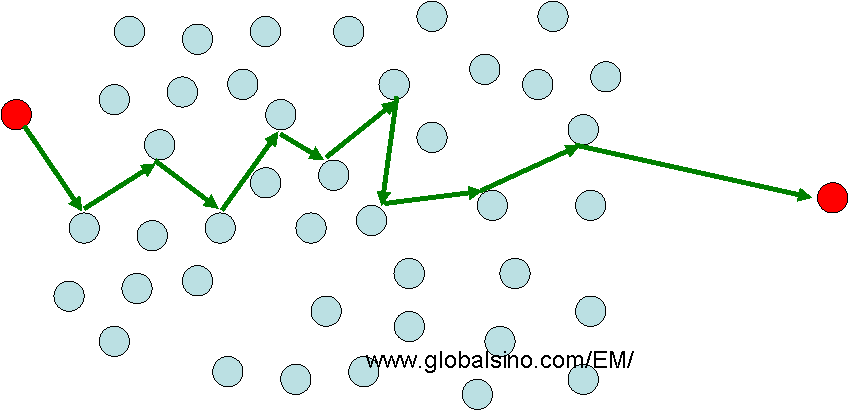
Figure 4476a. All particles, including electrons, suffer from collisions with atoms such that their path through
space between atoms is short. The typical path length is called the mean free path.
The inelastic mean free path (IMFP) is a concept of how far an electron can travel through a thin film or a near surface region of a solid before losing its energy. The major energy loss of a monochromatic primary electron beam is because the electrons interact strongly with matter, leading to plasmon excitation, electron-hole pair formation, and vibrational excitation. IMFP is a basic parameter for quantification of spectroscopes and for determining the surface composition and the mean
escape depth (MED) of the analysis [11], based on interaction with energetic electrons, such as Auger electron spectroscopy
(AES), X-ray photoelectron spectroscopy (XPS), and electron energy loss spectroscopy (EELS). The IMFP can be measured [1] or calculated with various theoretical models [2–5], e.g. Monte Carlo (MC) calculations. Ignoring the effect of electron diffraction, the intensity of the primary electrons, I0, is damped as a function of the distance, d, into the solid. The intensity decay can be given by,
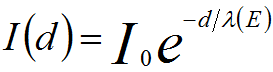 ---------------------------------- [4476a] ---------------------------------- [4476a]
where,
I(d) -- The intensity after the primary electron beam has traveled through the solid.
λ(E) -- The inelastic mean free path (IMFP).
E -- The energy of incident electron beam (keV).
Therefore, λ can be calculated as,
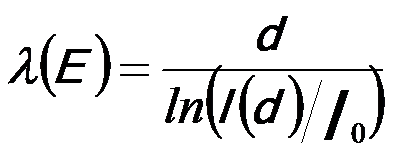 ---------------------------------- [4476b] ---------------------------------- [4476b]
where,
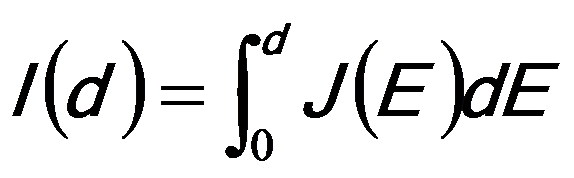 ---------------------------------- [4476c] ---------------------------------- [4476c]
J(E) -- The EEL spectrum.
Note that in the case of EELS measurements based on TEM specimen, d is the thickness of the specimen (t).
According to theoretical calculations, for organic materials the mean free path (MFP, λ) can be given by [12],
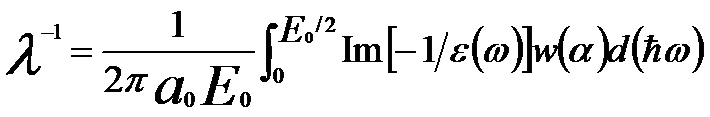 ------ [4476d] ------ [4476d]
λ(E) is defined as the distance of which an electron beam can travel before its intensity decays to 1/e of its initial value. The IMFP for insulators and semiconductors can be calculated by [9],
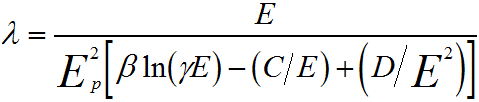 ---------- [4476e] ---------- [4476e]
where, the parameters
are defined by,
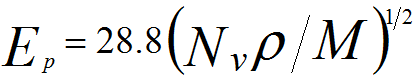 ---------------------- [4476f] ---------------------- [4476f]
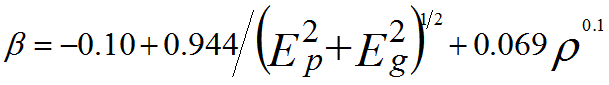 ------------ [4476g] ------------ [4476g]
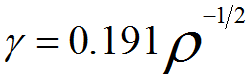 ---------------------------------- [4476h] ---------------------------------- [4476h]
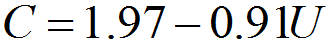 ------------------------------- [4476i] ------------------------------- [4476i]
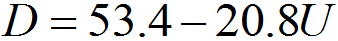 ---------------------------------- [4476j] ---------------------------------- [4476j]
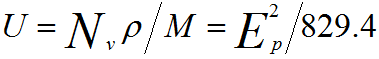 ---------------------- [4476k] ---------------------- [4476k]
where,
Nv -- Number of valence electrons per atom or molecule
ρ -- Material density (in g/cm3)
M -- Atomic or
molecular weight
Eg -- Band-gap energy (in eV) for insulators and semiconductors
Based on the Kier–Hall
molecular indices [7 - 8], Cumpson [6] developed an expression for predicting IMFP values for polymers and other organic materials, given by (Assuming E = 1 keV),
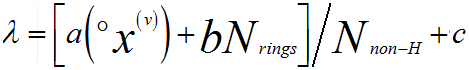 ------------ [4476l] ------------ [4476l]
where, °χ(v) -- Zero-order or atomic connectivity indices of Kier
and Hall, evaluated by Bicerano’s method [7]
Nnon-H -- Number of atoms in the molecule or
polymer repeat unit, excluding hydrogen atoms (for polymer)
Nrings -- Number of six-member aromatic rings in the molecule or polymer
repeat unit
a, b, c -- Fitting parameters
Equation [4476l] can easily be extended to other electron energies using the power law
dependence of the IMFP, given by,
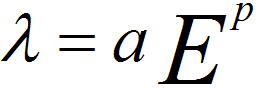 ------------------------------ [4476m] ------------------------------ [4476m]
where a and p are the constants
The exponent p varies in a
wide range. It was found that p is 0.7665 [10] and 0.79 [3] for organic compounds and the group of
14 organic compounds, respectively.
Other useful methods were derived for predicting IMFP values for inorganic and organic materials by Gries [5] based on an orbital model and by Ashley and Williams [2] for the IMFP of electrons in solid organic insulators. Figure 4476b shows energy dependence of the inelastic mean free paths derived from different methods and obtained by experiments. More values have been listed on Electron Inelastic Mean Free Path of Elements and Compounds.
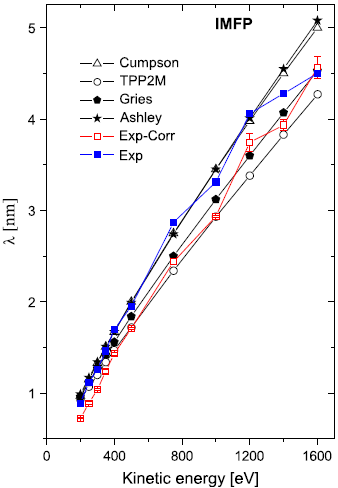
Figure 4476b. Energy dependence of the inelastic mean free paths for
poly[methyl(phenyl)silylene] films
derived from different methods and obtained by experiments [9].
Egerton [13] also presented a simplified expression for the IMFP (in nm),
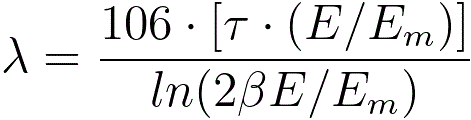 ------------------ [4476n] ------------------ [4476n]
Em = 7.6 x Z0.36 ------------------ [4476o]
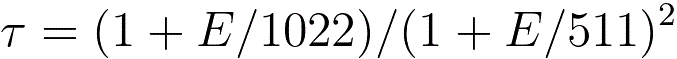 ------------------ [4476p] ------------------ [4476p]
where,
Z -- The average atomic
number.
β2 -- The collection angle (mrad).
τ -- A relativistic
correction factor.
Equation 4476n can be computed with a DM script (including calculation of average electron energy loss). Mean free path of inelastic electron scattering λ practically depends on three major factors: atomic density, number of “free” electrons per atom, and contribution of atomic core-loss transitions. Two major λ(Z) behaviors are periodic oscillation and smooth increase approximated as 1/λ= Nσ ~ Za. Here, a is a constant.
[1] Powell CJ, Jablonski A. J Phys Chem Ref Data 1999;28:19–62.
[2] Ashley JC, Williams MW. Radiat Res 1980;81:364–73.
[3] Tanuma S, Powell CJ, Penn DR. Surf Interface Anal 1994;21:165–76.
[4] Cumpson PJ. Surf Interface Anal 2001;31:23–34.
[5] Gries WH. Surf Interface Anal 1996;24:38–50.
[6] Cumpson PJ. Surf Interface Anal 2001;31:23–34.
[7] Bicerano J. Prediction of polymer properties. 2nd ed. New York: Marcel Dekker;
1996.
[8] Kier LB, Hall LH. Molecular structure description. San Diego, CA: Academic
Press; 1999.
[9]
J. Zemek, J. Houdkova, P. Jiricek, A. Jablonski, V. Jurka, J. Kub, Determination of electron inelastic mean free paths for poly[methyl(phenyl)silylene] films, Polymer 50 (2009) 2445–2450.
[10] Jablonski A. Surf Interface Anal 1993;20:317–21.
[11] ASTM Standards E673-95c, Annual Book of ASTM
Standards, American Standards for Testing and Materials,
Vol. 3.06, West Conshohocken, PA, 1997, p. 907.
[12] Zhenyu Tan, Yueyuan Xia, Mingwen Zhao, and Xiangdong Liu, Electron stopping power and inelastic mean free path in amino acids and protein over the energy range of 20–20,000 eV, Radiat Environ Biophys (2006) 45: 135–143.
[13] R.F. Egerton. Electron Energy-Loss Spectroscopy in the electron microscope. Plenum
Press, New York, 1996.
|