Digital-Filtered Least-Squares Peak Fitting for EDS Quantification - Practical Electron Microscopy and Database - - An Online Book - |
||||||||
| Microanalysis | EM Book http://www.globalsino.com/EM/ | ||||||||
| ================================================================================= | ||||||||
In the quantifications in electron- and photon-induced X-rays, linear least-square fitting can be used to deconvolute the overlapped peaks once the continuum background is eliminated by a proper technique. Digital filter based on linear least-square fitting was first proposed in 1973. Filtered Least-Squares Peak Fitting method was then suggested to address the problems related to absorption edges in the continuum and to the inaccuracy induced by peak overlapping. Therefore, the X-ray (e.g. EDS) quantitative results can be derived from the “filtered” intensity values ratioed to the appropriate X-ray continuum regions through a least squares fitting formula rather than plotting the proportions of the net intensities in a ternary system. [1] The filter-fitting method addresses the problem of continuum removal by transforming the measured spectra into a set of
related spectra to which least-squares fitting may be directly applied. Note that the continuum of a spectrum presents slow variation
with energy, while the peaks of the spectrum show much faster variation. A digital filter operator is a simple correlating
array-function which is used to: Therefore, after the filtering, no errors are introduced into the next analysis processes. In this digital filtering method, a set of coefficients are multiplied against corresponding channels of the spectrum. The sum of these products can be given by, [1] Figure 1761a illustrates a simple case of digital filtering on which has a Gaussian peak with a straight linear background. The main (central) lobe consists of positive coefficients, while the side-lobes contain negative coefficients. There is a strong response to the peak in the filtering, while the straight linear components are suppressed to zero exactly. Figure 1761a. Schematic illustration of a simple case of digital filtering. Adapted from [1] Figure 1761b shows the digital filtering on a spectrum with two Gaussian peaks and smooth continuum traces. It is clear that the filtering introduces distortions to peak shapes. Forturnately, this distortion is predictable and consistent, and does not alter the main information of the peaks. On the other hand, the filtering is a linear operation, i.e. a composite spectrum is the linear sum of its individually filtered peak components. Finally, the contribution of the filtered continuum is zero and can be ignored.
No matter how different the initial spectra are before filtering, the continuum will be effectively suppressed and only the peak structures remain after filtering. Figure 1761c shows an example of digital filtering on a EDS profile.
Due to the linearity characteristics of the filtering method, a conventional least squares fitting procedure can be applied to obtain the best fit of peak structure if both the measured data and the reference peaks are digitally filtered. In this fitting method, it is assumed that the measured reference spectra provide accurate peak models. Furthermore, the computed results can only be accepted if the errors are less than certain values. Therefore, it is important that the filtering procedure outputs the statistical uncertainty of the results (see page2513). In ideal least-squares fitting, if the Chi-Squared (x2) is normalized (dividing by the number of fitted points minus degrees of freedom), it should be approximately one in average. Values of x2 that are much greater than one indicates some systematic error in the fit. However, we need to keep in mind that there may be two problems which digital filtering cannot fully deal with:
[1] McCarthy, J.J., and F.H. Schamber, 1981, Least-Squares Fit with Digital Filter: A Status Report. In Energy Dispersive X-ray Spectrometry, edited by K.F.J. Heinrich, D.E. Newbury, R.L. Myklebust, and C.E. Fiori, pp. 273-296. National Bureau of Standards Special Publication 604, Washington, D.C.
|
||||||||
| ================================================================================= | ||||||||
|
|
||||||||
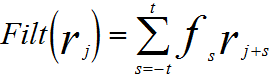 ----------------------- [1761]
----------------------- [1761]