SiGe and SiGe/Si Systems and its Defects

Chapter/Index: Introduction | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | Appendix

SiGe and SiGe/Si Systems and its Defects

The lattice constant of fully relaxed Si_1-xGe_x crystal (a_SiGe) is given by the modified Vegard's law,
          a_SiGe = a_GeX + a_Si(1-X) - 0.0272 X(1-X)
                    = 0.5431 + 0.01992 X + 0.002733 X² (nm) ---------------------- [3380a]
where,
          a_Ge -- The lattice constant of pure Ge crystal.
          a_Si -- The lattice constant of pure Si crystal.

Or, the lattice constant of a SiGe alloy can be given by,

---------------------- [3380b]

where,

is the mole fraction of silicon (Si) in the SiGe alloy.
a_Si = 5.431 Å.
a_Ge = 5.658 Å.

As discussed in page3381, for the (001) SiGe/Si system in which the primary misfit dislocations are <110>{111}, the critical thickness h_c of SiGe epitaxial layer without misfit dislocations can be given by, [1]

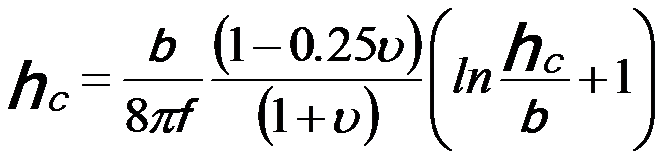critical thickness of lattice-mismatched Epitaxial Alloy ---------------- [3380c]

However, the actual lattice-mismatched SiGe films can be grown thicker than predicted without misfit dislocations. The empirical critical thickness is approximately 1.65 times that predicted by Equation 3380c.

Other factors can also determine the defect density in the strained epitaxial films. For instance, the defect density decreases as the single crystal area decreases.

Figures 3380a and 3380b show the features of dislocations in SiGe epitaxial films on Si substrates depending on the sizes of the active areas of microelectronic devices. The black surroundings are Si substrate.

Dislocations in smal active areas: (a) Stressed-isolation wafer with 0% Ge

Figure 3380a. Dislocations in smal active areas: (a) Stressed-isolation wafer with 0% Ge, (b) Relaxed-isolation wafer with 13% Ge, after the 950 °C anneal. Adapted from [2]

Dislocations in large active areas

Figure 3380b. Dislocations in large active areas (37 µm x 180 µm): (a) Stressed-isolation wafer; (b) Stressed isolation wafer with 0% Ge after the 950 °C anneal. Note that the arrows indicate the dislocation loops at the edge of the active areas. The density of dislocations at the isolation edge is high and there is no dislocations in the center region. Adapted from [2]

Table 3380. Comparison of properties of crystalline and amorphous SiGe materials.

	Crystalline SiGe	Amorphous SiGe
Energy gap/Optical band gap E_g(eV)		1.50 for a-Si_1-xGe_x:H
Urbach energy E₀ (meV)		50 for a-Si_1-xGe_x:H
Fermi level density of states g (E_F) (cm^-3eV^-1)		10¹⁶ for a-Si_1-xGe_x:H

[1] S. R. Stiffler, J. Comfort, C. L. Stanis, D. L. Harame, E. de Frésart, and B. S. Meyerson, J. Appl. Phys. 70, 1416 (1991).
[2] K. Schonenberg, Siu-Wai Chan, D. Harame, M. Gilbert, C. Stanis and L. Gignac, The stability of Si1−xGex strained layers on small-area trench-isolated silicon, Journal of Materials Research, 12(02) (1997), pp 364-370.

Practical Electron Microscopy and Database

An Online Book, Second Edition by Dr. Yougui Liao (2006)

SiGe and SiGe/Si Systems and its Defects