In EELS elemental analysis, the most common implementation of a power law fit (or so-called single scattering power law fit) is a linear least squares fit to the log-log
transform over an energy region immediately
preceding the ionization threshold of the experimental spectrum. The power law fit is based on the asymptotic behaviour of analytic functions describing the plasmon peak (Drude model) and core-loss excitations (hydrogenic cross section). The power law profile in a spectrum is fitted in the pre-edge region and extrapolated to the post edge region. The core-loss intensities are extracted by straightforward subtraction of the background intensity from the acquired signal.
As shown in Figure 3419a, in EELS quantitative analysis, this background contribution Ib must be subtracted to obtain the core-loss signal Ik,
Ik = It - Ib ------------------------------------------- [3419a]
where,
It -- the total integrated intensity over the core-loss integration range.
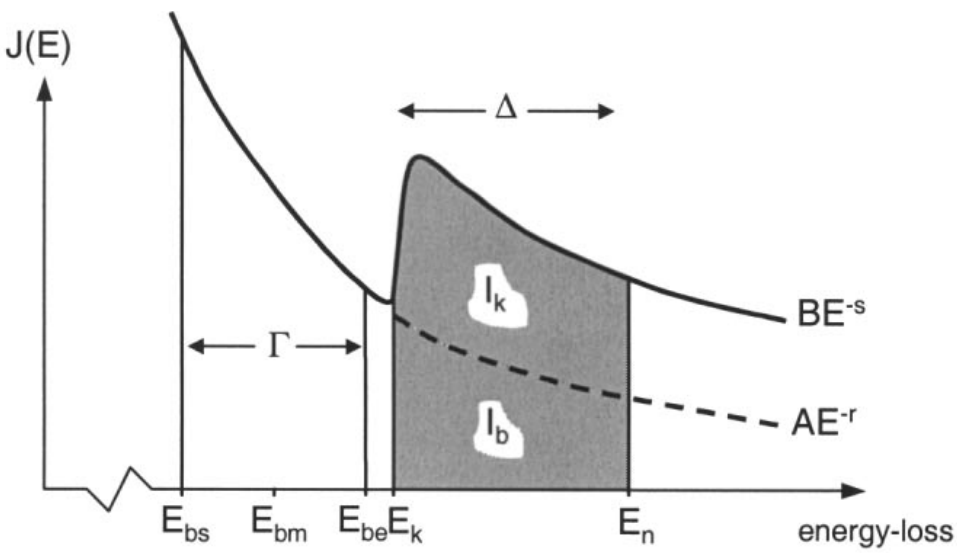
| Figure 3419a. Schematics illustrating the extrapolation of the
characteristic background signal Ib to leave the core-loss signal Ik using power-law fit. [25] |
The background removal procedure is normally performed by an extrapolation method suggested by Egerton [1]. The inverse power law can be used to fit the pre-edge region (i.e. immediately prior to the onset of the edges), which is given by,
IB(E) = AE-r ----------------------- [3419b]
where,
E -- Transmitted electron energy loss of each channel.
IB -- Intensity of the background in the channel of energy loss E.
A -- A fitting constant (coefficient) for a particular curve fit (A: broad), which determines the intensity of the background.
r -- Exponent (a fitting constant) for the curve fit (r = 2 ~ 6), which is responsible for the curvature of the fitting curves.
Both A and r can be determined by least-squares curve
fitting of experimental background IB(E) at energy losses just below the ionization
threshold, and they can vary across the specimen,
as a result of changes in thickness and composition, and depend on experimental conditions [20, 21]. For instance, in two-window method, the background-fitting simply divides the
fitting region into two sections of equal
width [16, 24] as shown in Figure 3419b. Then, by applying least-squares fitting, the values of r
and A may be obtained by the approximate
formulae [16],
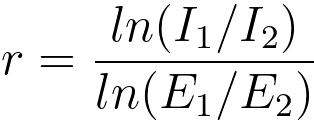 ------------------------------------------------ [3419c] ------------------------------------------------ [3419c]
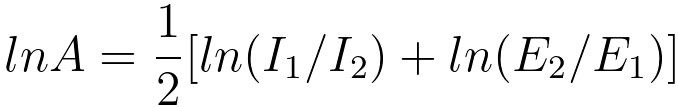 -------------------- [3419d] -------------------- [3419d]
where,
I1 and I2 -- the pre-ionisation edge integrals,
E1 and E2 -- the energies corresponding to the pre-edge region mid-points.
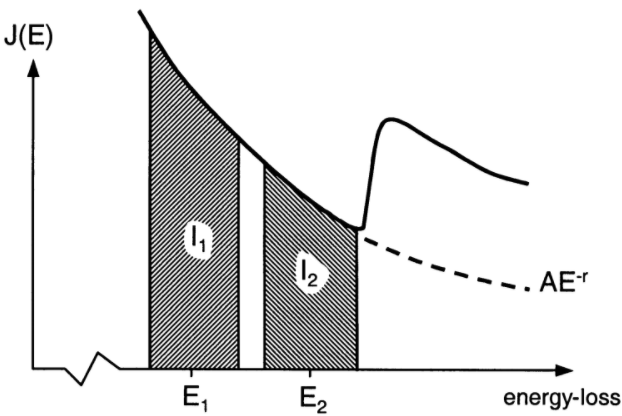
| Figure 3419b.
Background extrapolation using the two-window method.
The background-fitting region consists of two regions of equal energy
width. [25] |
The coefficient A especially varies
strongly on beam current or exposure time, and thus the intensity of the background-fitting region, while the
value of r tends to increase with increasing energy loss and decreases with increasing sample thickness and collection angle. The EELS
intensity, IB(E), is extended using the Power-law with a negative exponent that decays
smoothly to zero at high energies E. These dependencies require the spectrum background to be fitted at each core-loss edge separately. This fit has an assumption that the background intensity has the same energy depen
dence over the entire core-loss edge energy range. The main drawback to this method is the fact, that there is very little physical justification of the assumption for the power-law dependence of the background. In DigitalMicrograph (DM) operation, one does not have prior knowledge about the power-law fitting constants (A and r) when the power-law fit is used.
The goodness ( χ2) of fit is defined by linear-squares fit to the experimental spectrum. The fit is subtracted from the total spectrum intensity and is extrapolated beyond the edge to give the core-loss signal, and the background is subtracted on the assumption that the fitting
parameters A and r remain constant. Due to this assumption and noise in the fitted
experimental data, this procedure contains some incertitude. Note that the power law form in Equation 3419b is widely used to remove the background because it contains only two parameters to be adjusted and it yields a good fit in many cases.
Different ways of adjusting the two parameters (A and r) are normally used:
i) 2-area method procedure [1],
ii) Rravine-search procedure [2],
ii) and simplex procedure [3 - 4].
Similarly, the background intensity after an energy loss beyond the ionisation edge can also be given by the power-law relation, [23]
I(E) = BE-s ----------------------- [3419e]
where,
B -- a background scaling constant,
s -- the
post-edge slope exponent.
At
low energy core-losses (e.g. < 80 eV), the inverse power
law is less appropriate and more complicated functions
may be required.
The statistical errors in background extrapolation are described by
the parameter h in the estimation of the SNRpl, given by,
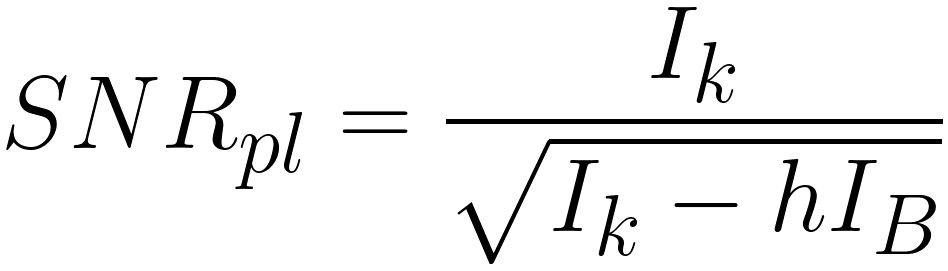 ----------------------- [3419f] ----------------------- [3419f]
where,
IK -- The integral intensity of the signal,
IB -- The integral
intensity of the background.
h -- The dimensionless parameter (typically in the range of 2~30) which depends strongly on the width of the fitting areas (pre-edge window(s) and signal window) and accounts for the statistical
uncertainties associated with the background subtraction
(variances of IB), and thus it involves the error by which the background dependent part is increased due to extrapolation errors (page4719). h is given as,
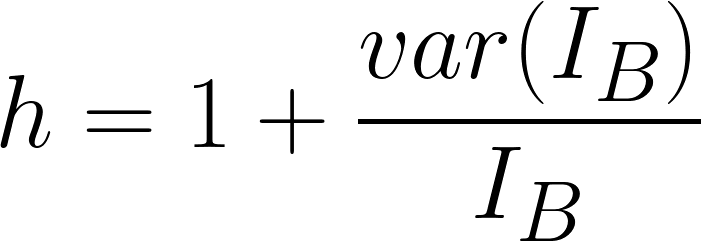 ---------------------------------- [3419g] ---------------------------------- [3419g]
In order to
obtain reliable elemental maps that are free from artifacts and systematic errors, a careful choice of the background removal procedure is always needed.
For the single scattering spectrum, the overall intensity of the spectrum (details at page1390) can be given by,
I = (AE-r + p1σ1(E) + p2σ2(E) + ... + pNσN(E)) -------- [3419h]
where,
p1~ pN -- The probability of scatterings,
σ1~ σN -- The cross sections from different elements.
When this power-law technique is used to remove the background of ELE spectrum, obtaining an accurate removal, in some cases, is very difficult and even it fails. However, this method works well for a major edge, easily visible above the background. In summary, it can give a very good fit only when:
i) The width of the energy window chosen to fit the power law function is chosen wisely. The energy window should be chosen to be sufficiently large to minimize the background extrapolation error. Indeed, a small variation in the energy width or position of the background fitting region can lead to
dramatically different results.
ii) The preceding edges is not too far away from the fitting window. The
further away from the fitting region, the larger will the systematic errors be.
iii) The TEM sample is not too thick (Plural scattering contribution is negligible if t/λ < 0.5). Plural scattering processes that are more probable in thicker TEM samples (t/λ > 1), lead to deviations of the background shape from the power law.
iv) The energy window for background fitting does not contain any extended fine structure of preceding edges of other elements and is not on minor edges present before the
edge.
v) The data is not very noisy.
vi) The atomic percentage of the element is not too small. It can be problematic for a weak edge arising from the
presence of small atomic percentage of an element in the material.
vii) The spectrum has no overlapping with other major edges.
viii) The energy separation of edges are large enough. For instance, it is not applicable to analyze boron (B) in Ni3B
and Ni20.3Ti2.7B6 materials because of the presence of the large Ni M-edges. [14,15]
ix) The analyzing edges are not low energy edges below 60 eV, e.g. it does neither work for the extraction of complex plasmon background nor work for K edge (55 eV) of Li element.
Since the background may vary across
the specimen due to changes in composition and thickness, for elemental maps, the background must be
subtracted for every single pixel of a core-loss image. Figure 3419c shows the oxygen (O) elemental maps obtained with both power-law fit and multiple linear least-squares fit. The measured materials is Ca/TiO.
It shows that the extracted net intensities in the area on right-hand side differ by as much as 30%, and the O map obtained with MLLS fit can differentiate the oxygen levels in different areas clearer than that with power-fit.
.
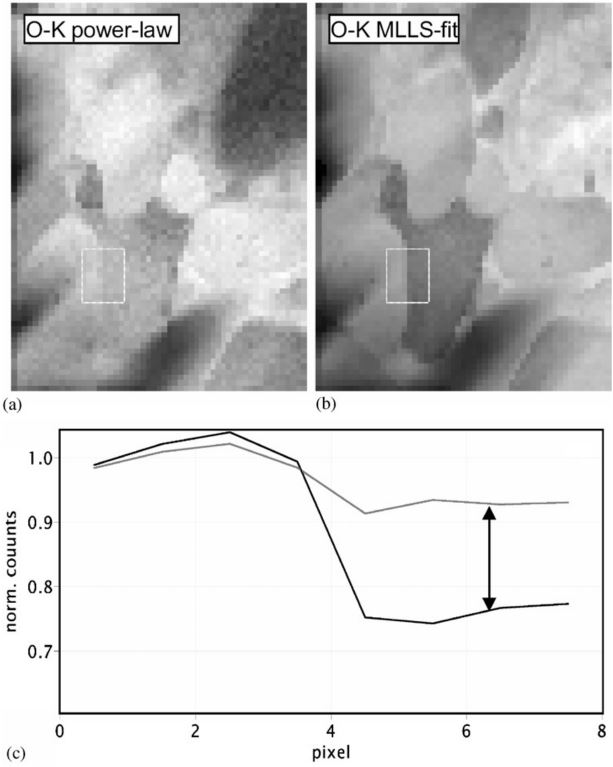
| Figure 3419c. Oxygen elemental maps obtained with power-law fit (a) and multiple linear least-squares fit (b).
The extracted net intensities differ by as much as 30% (c). The measured materials is Ca/TiO. [12] |
In the cases that very thick TEM samples are used in EELS or EFTEM measurements, the increase of plural scattering effects induces two main problems:
i) The background models, e.g. the form of power law, are not convenient to represent the actual background;
ii) The low energy edge onsets are embedded in the background, meaning some edge becomes invisible.
A few criteria may be performed to achieve a good fit with power-law fit:
i) The high energy end of the fitting region should be
placed as close to the edge threshold as possible, but the edge onset should be avoided. This energy region close to the edge onset has the greatest influence on the accuracy of the extrapolation procedure
[16].
ii) The energy width of the fitting region should be as large as possible in order to minimize the statistical error of the measurement [17].
In power law fit, choosing a suitable window in order to fit the background is challenging or sometimes in question [5-11]:
i) Extrapolation under the excitation edge can make the outcome quite sensitive to the choices of window position and window width.
ii) The assumption of the power law background is known to fail for wide energy regions because the parameter r of the power law, in Equation [3419b], is not constant
over a wide energy region. Therefore, the fact that r changes with energy,
meaning that the power law function is not a good approximation to model an
experimental background over a wide energy range. For this reason, some other models have been proposed:
ii.a) Power law with polynomial exponent 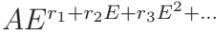 , ,
ii.b) Exponential background Aexp(-αE).
Furthermore, in general, the energy window under which the power
law is fitted must be:
i) Large enough (> 50 eV) to ensure
reasonable precision. However, there are still some exceptions, for instance, for a core loss of the interesting element is about 348 eV, a small background window (e.g. 20 eV) is used to fit the spectrum in order to avoid the contribution from the carbon edge (284 eV), so that we only pick up the signal generated by the interesting element for the elemental evaluation.
ii) Not too wide (< 200 eV) becasue:
ii.a) The
power law is only valid over a restricted energy range,
ii.b) The energy peaks of other possible elements in the specimen are very close to the core-loss of the interesting element.
Since an inverse power-law does not decay as rapidly as an exponential function, it is very common that the AE-r extrapolation gives rise to a
background that intersects the data at some energy not
very far above the core-loss edge, resulting in negative core-loss
intensity after background removal. The error in quantification will be worse when dominant bulk plasmon peak
and plural scattering present. Such problems can be avoided by using some ‘smart’ background-subtraction algorithms (refer to page3936).
In general, if the TEM specimen is too thick (t/λ > 0.4), a deconvolution process must be employed to remove the effect of plural scattering, since the increase of plural scattering intensity in the higher energy region of an ionization edge can cause some artifacts:
i) Mask the fine structure;
ii) Make the background signal on subsequent edges deviate significantly from the power law model.
In this case, in order to deconvolute the core-loss spectrum, the Fourier-ratio method is applied. The deconvolution procedures then are:
i) Collect both the low- and core-loss spectra from the same region of the specimen under the same conditions (including eV/change, convergence and collection semiangles).
ii) Isolate the edge of interest and remove the background intensity.
iii) Fourier-transfer the low-loss spectrum and background-subtracted edge.
iv) Divide the core-loss spectrum Fourier transform by the low-loss Fourier transform.
v) Inverse the Fourier transform to yield the desired deconvolved spectrum.
In order to overcome these difficulties of weak EELS signals, standard edge and convolution
techniques [18, 19] have been used in low concentration quantifications.
However, in most cases, recording low-loss and core-loss spectra under the same conditions is extremely challenging, since the acquisiton time required for a good SNR (signal to noise ratio) in the core-loss spectrum is usually not short enough to avoid saturation of the signal from the ZLP (zero-loss peak). Therefore, in practice, it is necessary to sacrifice the SNR in the core-loss signal, or utilize a spectrometer system that has an ultrafast electrostatic shutter installed.
Some methods have been proposed to test the validity of elemental maps obtained from power-law fit:
i) The presence of elemental quantities.
ii) The absence of detection where no element is present. In this case, the gray level after background correction should be zero on average.
iii) Evaluate a chi-square measure at each image point after the fitting procedure to test the goodness-of-fit of the power-law function to the data. [13]
[1] Egerton R.F., Electron Energy Loss Spectroscopy in the Electron Microscope (NewYork,
Plenum Press, 1986).
[2] Bevington P.R., Data reduction and error analysis in the physical science (McGraw-Hill,
New York, 1969), p. 105.
[3] Colliex C., Jeanguillaume C. and Trebbia P., Microprobe Analysis of Biological Systems,
Hutchinson and Somlyo Eds. (Acad. Press, New york, 1981), p. 251.
[4] De Bruijn W., Ketelaars D., Gelsema E. and Sorber L., Microsc. Microanal. Microstruct.
2 (1991) 281.
[5] R. F. Egerton, M. Malac, Ultramicroscopy 92 (2002) 47-56.
[6] D. S. Su, E. Zeitler, Phys. Rev. B vol 47-22 (1993) 14734-14740.
[7] T. Pun, J. R. Ellis, M. Eden, Journal of Microscopy 135 (1984) 295-316.
[8] T. Pun, J. R. Ellis, M. Eden, Journal of Microscopy 137 (1985) 93-100.
[9] R. F. Egerton, Ultramicroscopy 9-4 (1982) 387-390.
[10] M. Unser, J. R. Ellis, T. Pun, M. Eden, Journal of Microscopy, 145 (1987)
245-256.
[11] D. R. Liu, L. M. Brown, Journal of Microscopy 147 (1987) 37-49.
[12]
Gerald Kothleitner and Ferdinand Hofer, Elemental occurrence maps: a starting point for quantitative EELS spectrum image processing, Ultramicroscopy 96, 491–508 (2003).
[13] C. Colliex, C. Jeanguillaume, and P. Trebbia, “Quantitative local microanalysis
with EELS” in: Microprobe Analysis of Biological Systems, (ed.) by T. E.
Hutchinson and A. P. Somlyo Academic Press, New York (1981) pp. 251–271.
[14] J. Bentley, G. L. Lehman, and P. S. Sklad, “Background Fitting for Electron
Energy Loss Spectra,” Analytical Electron Microscopy-1981, p. 161, ed. R.H.
Geiss (San Francisco Press, San Francisco, 1981).
[15] J. Bentley, G. L. Lehman, and P. S. Sklad, “Alternative Background Fitting for
Electron Energy Loss Spectra,” Proc. 40th Ann. Meet. Electron Microscopy Soc.
Am., p. 496, ed. G. W. Bailey (Claitor’s Publishing Div., Baton Rouge, 1982).
[16] A. Berger and H. Kohl, “Optimum imaging parameters for elemental mapping
in an energy-filtering transmission electron microscope,” Optik 92, 175–193
(1993).
[17] T. Pun, J.R. Ellis, and M. Eden, “Optimized acquisition parameters and statistical detection limit in quantitative EELS,” J. Microsc. 135, 295–316 (1984).
[18] Shuman H. and Somlyo A.P., Ultramicroscopy 21 (1987) 23.
[19] Leapman R.D. and Swyt C.R., Ultramicroscopy 26 (1988) 393.
[20] Leapman, R. D., and Swyt, C. R., Electron energy-loss imaging in the STEM – Systematic and statistical errors. In Microbeam Analysis – 1983, ed. R. Gooley, San Francisco Press, San Francisco, CA, pp. 163–167, (1983).
[21] Leapman, R. D., Gorlen, K. D., and Swyt, C. R., Background subtraction in STEM energy-loss mapping. In 42nd Ann. Proc. Electron Microsc. Soc. Am., ed. G. W. Bailey, San Francisco Press, San Francisco, CA, pp. 568–569, (1984).
[22] R.F. Egerton, Electron Energy-Loss Spectroscopy in the
Electron Microscope (Plenum Press, New York, 1996).
[23] D.C. Joy, A.D. Romig and J.I. Goldstein (eds.), Principles of
Analytical Electron Microscopy (Plenum Press, New York,
1986).
[24] R.F. Egerton, in: Microbeam Aanlysis, ed. K.F.J. Heinrich (San
Francisco Press, San Francisco, 1982) p. 43.
[25]
P. J. Thomas and P. A. Midgley, An introduction to energy-filtered transmission electron microscopy, Topics in Catalysis, 21(4), (2002) 109.
|
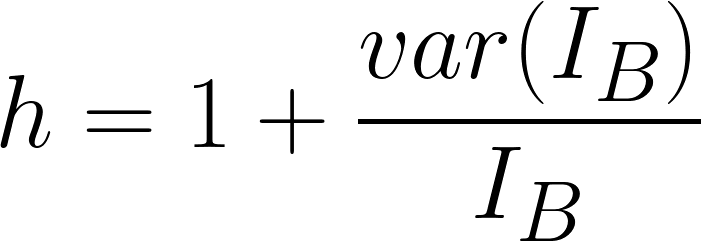 ---------------------------------- [3419g]
---------------------------------- [3419g]