=================================================================================
Similar to incident x-rays, energetic incident electrons can also interact with electrons in materials. This process results in an amount ħq of momentum being transferred to the sample. In EELS measurements, the electron interaction is due to coupling between the electrons which may have the form, [1]
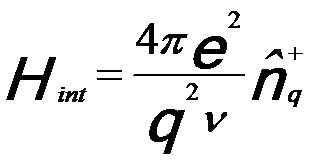 ------------------------------ [3375a] ------------------------------ [3375a]
where,
ν -- A normalization volume for the probe electron [2];
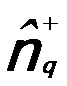 -- The density
fluctuation operator, given by, -- The density
fluctuation operator, given by,
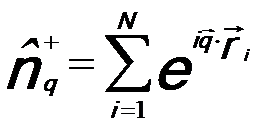 ------------------------------ [3375b] ------------------------------ [3375b]
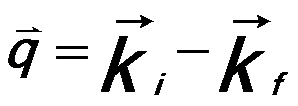 ----------------------------------------- [3375c] ----------------------------------------- [3375c]
Therefore, the double differential scattering cross-section (DDSCS) for inelastic electrons from the ground state |ψi> of the Hamiltonian H0 by applying Fermi's golden rule can be given by,
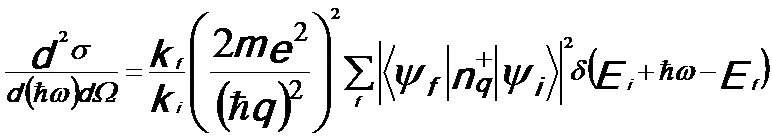 -------- [3375d] -------- [3375d]
where,
ħω -- The energy lost by the probe electron scattered into solid angle;
m -- The mass of the electron;
Finally, the EEL spectrum can be described in a dielectric formulation [3] by,
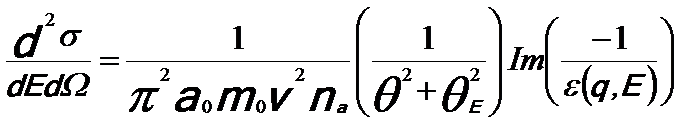 -------- [3375e] -------- [3375e]
where,
v -- The speed of the incident electron.
na -- The number
of atoms per unit volume.
θE -- The characteristic scattering angle (θE = E/γm0v2 = E/mv2/2E0).
Im(−1/ε) -- The energy loss function.
a0 -- Bohr radius.
σ -- The total scattering cross section.
Ω -- The solid angle.
Equation 3375e fundamentally presents the probability of a specific scattering event in materials, expressed by the scattering cross-section. This also is the most fundamental equation of EELS. Based on Equation 3375e and a Kramers–Kronig analysis, the complex dielectric function ε = ε1 + iε2 can be obtained from the low-loss EEL spectrum.
For small scattering angles (q → 0), the energy- differential cross-section, up to a collection angle β, can be given by, [7]
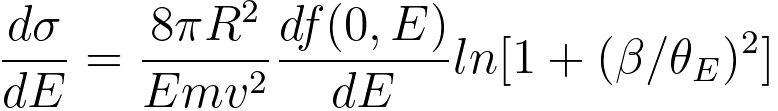 ------------------------ [3375f] ------------------------ [3375f]
where,
v -- the velocity of the incident electron,
m -- the mass of the incident electron,
R -- the Rydberg energy (see page4433),
E0 -- the incident electron energy.
Equation 3375f is valid within the dipole region, where the GOS (generalised oscillator
strength) may be approximated to the optical value f(0,E).
In EELS experimental measurements, the number of atoms in the beam corresponding to, as a function of the core-loss inelastic cross-section, can be given by, [4]
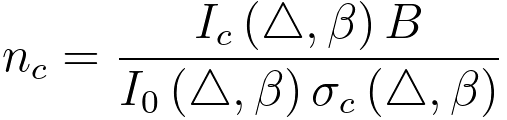 -------------------------------------- [3375g] -------------------------------------- [3375g]
where,
Δ -- a same energy window above the zero-loss peak and core-loss,
Ic(Δ,β) -- the number of
counts into a core-loss edge, i.e. the number of counts
above the edge after background is subtracted,
I0(Δ,β) -- the number of counts in the energy window Δ above the zero-loss peak,
σc(Δ,β) -- an appropriate inelastic cross-section obtainable either from theory or from a standard,
β -- the collection semi-angle of EELS,
B -- the effective area of the electron beam.
Table 3375 lists the energy losses and scattering angles of various inelastic electron scatterings in electron interaction with materials.
| Table 3375. Energy losses and scattering angles of various inelastic electron scatterings in electron interaction with materials. |
| Process |
Phonon excitation |
Plasmon excitation (oscillation):
(Introduction)
(Theory) |
Direct radiation losses |
Inner shell ionization |
| Electrons in outermost shell: only weakly
bound to atoms but are coupled to each other by electrostatic
forces |
Intraband transitions |
Bremsstrahlung radiation due to deceleration of the electron beam in the Coulomb field of an atom |
Core-loss |
| Electrons in valence band |
Electrons in conduction band |
| Interband transitions |
Excitation of loosely bound electrons in conduction band, leading to secondary electrons (SEs) emissions |
| Thermal diffuse scattering, heating |
Main transitions of valence electrons [5] |
| Special note |
It normally cannot be resolved in EELS due to the energy spread of the electron
source |
~20% contribution of peak broadening in EELS at large scattering angles (> 20 mrad) [5] |
Most SEs have
a kinetic energy of <50 eV; The resulting SE distribution is peaked at 3 to 5 eV, with the
distribution decreasing sharply as the energy
increases above 5 eV |
|
|
|
| Region of
energy loss |
Low loss
(< 50 eV) |
Low loss
(< 50 eV): Energy loss is low because these electrons require only small amounts of energy for excitation due to loosely bound |
|
|
High loss
(> 50 eV) |
| Energy loss E [eV] |
20 meV–1 eV |
3 - 25 |
|
|
10 - 2000 |
| |
|
Controlled by the density of loosely bound states |
|
|
|
| Materials |
|
Predominant in insulators and semiconductors |
Predominant in metals |
|
|
|
| EELS background |
|
Predominated by interband transitions of the valence electrons in the absence of
plural plasmon scattering, i.e. in sufficiently thin samples [5] |
|
|
|
|
| EELS broadening |
|
Main origin of peak broadening in EELS [5] |
|
|
|
| Interaction |
|
Most common inelastic interaction due to high free electron density;
Inelastic scattering is mainly brought
about by the collisions with the loosely bound solid-state electrons |
|
|
|
| Scattering angle θE [mrad] |
5 - 15 |
< 10 |
|
|
0.1 - 10 |
| Oscillation |
Collective oscillations of atoms (e.g. lattice vibrations) |
Collective oscillations of free electrons, a quantum
of a collective longitudinal
wave in the electron gas of a
solid |
|
|
|
| Detectability by EELS |
Is not resolved |
Yes |
|
|
Yes |
| Effects |
Causes specimen to heat up |
|
|
|
|
|
| Time |
|
Damped out in < 10−15 s |
|
|
|
| Localization |
|
Localized to < 10 nm |
|
|
|
| Cross sections |
|
Relatively large |
|
|
Relatively small |
Mean-free
paths |
|
Relatively short |
|
|
Relatively large |
| Intensity |
|
Much intense |
|
|
Much smaller |
| Modification |
Can reduce the number
of phonons by cooling the
specimen |
|
|
|
|
| Kikuchi patterns |
|
May be important in the formation
of Kikuchi patterns from light elements [6] |
|
|
|
| Characteristics |
Diffuse background, don’t carry any useful information |
Signature of the structure |
|
|
Elemental information |
[1] H. J. Hagemann, W. Gudat, and C. Kunz, Optical Constants from the Far Infrared to the X-ray Region: Mg, Al, Cu, Ag, Au, Bi, C and Al2O3, DESY SR-7417. Desy, Hamburg, W. Germany, 1974.
[2] W. S. M. Werner Surf. Interface Anal., vol. 31, p. 141, 2001.
[3] R. F. Egerton, Electron Energy Loss Spectroscopy in the Electron Microscope, Plenum Press, New York, 1996.
[4] A. P. Stephens, Quantitative microanalysis by electron energy-loss spectroscopy: Two corrections, 5 (1–3) (1980), 343-349.
[5] R. F. Egerton, Inelastic scattering of 80 keV electrons in amorphous carbon, 31(1), 1975, 199-215.
[6]
Philip, J. G., Whelan, M. J., And Ecerton, R. F.. 1974, Proc. 8th Int. Congress on
Electron Microscopy, Canberra. Vol. 1, p. 276.
[7] P.J. Thomas and P.A. Midgley, An introduction to energy-filtered transmission electron microscopy, Topics in Catalysis, 21 (4), (2002), 109.
|