=================================================================================
Electron microscopy (EM) analysis is based on the effects of elastic and inelastic scattering of an incident electron beam on interaction with atoms and the electrons of the material. The final signals used for image formation in the analyses are normally not the result of single scattering but of some electron diffusion caused by the gradual loss of the electron energy and by multiple scattering. Figure 3768a shows schematically the interaction processes and signals detected in different operating modes. The complete energy spectrum consists of primary electrons with the accelerating energy E0, emitted electrons, ions, heat, photons, and other internally generated signals. Generally, the rate of the input primary electrons is slightly larger than the sum of the rates of secondary, backscattered and transmitted electrons, this small change is due to the fact that part of electrons is absorbed into the sample that flow to the ground as indicated in Figure 3768b.
The response of incident energetic electrons to their interaction with the specimen is a function not only of energy loss due to inelastic interactions, but also of transferred momentum.
When incident electrons in EMs strike a specimen, they can undergo deceleration in the Coulombic field of the atoms, which is formed by the positive field of the nucleus (interaction with nucleus) and the negative field of the bound electrons (interaction with electrons).
| Figure 3768a. Products of interaction between incident electrons and matters. BSE: backscattered electrons; SE: secondary electrons; CL: cathodoluminescence; Auger electrons; EBIC: electron beam induced conductivity. |
Table 3768a. Signal per incident electron.
| Beam voltage |
20 keV |
| Secondary electrons |
0.6 |
| Backscattered electrons |
0.4 |
| Substrate atoms |
0 |
| Secondary ions |
0 |
| X-ray |
0.007 |
Table 3768b. Application of the products of interaction between incident electrons and matters.
|
Product |
Application |
Thickness dependence* |
| |
|
|
| Auger electrons |
Surface composition (surface sensitive: ~ 1 nm at surface, E ≤ 10 eV) |
N/A |
| Backscattered electrons |
Atomic number and phase differences (< 400 nm, 50 eV ≤ E ≤ E0) |
page1182 |
| Bremsstrahlung X-rays |
Background only (no application, < 2 µm, 0 < hν <E0) |
|
| Characteristic X-rays |
EDS for composition (< 2 µm, 0 < hν <E0) |
|
| Direct beam (transmitted beam) |
Morphological information in TEM mode (E ≈ E0) |
page1183 |
| Electron beam induced conductivity |
Electrical information |
|
| Electrons absorbed by lower pole piece |
No application |
|
| Electrons absorbed specimen |
EBIC (electron beam induced conductivity) |
page1184 |
| Electron-hole pairs |
| High-angle elastically scattered electrons |
Incoherent elastic scattering, atomic contrast in HAADF STEM imaging |
ADF STEM |
| Low-angle elastically scattered electrons |
Structural analysis and high resolution imaging; coherent elastically
scattered electrons; electron diffraction (e.g. CBED) |
page1183 |
| Inelastically scattered electrons in direct beam and diffracted beams |
Composition and bond states in EELS/EFTEM measurement (E = E0- ΔE, causing problems in TEM imaging); STEM and TEM (E ≤ E0) |
page1183 |
| Secondary electrons |
Topographical information; atomic number and phase difference (5~50 nm at surface, 0 eV < E ≤ 50 eV) |
|
Cathodoluminescence (CL)
|
UV, IR and visible light, electrical information, electronic states information (0 < hν < 1-10eV) |
|
| * TEM specimen thickness dependence |
Figure 3768b shows schematically the possible interaction processes between the incident electrons and an atom. The electron rays from A to F receive different responses because of the distance differences between their trajectories to the electron cloud and nucleus of the atom. Table 3768b lists the details of electron ray interactions with the atom and their corresponding products. The intensity of transmission (direct) beam will be reduced if the scattered electrons are removed from the transmitted beam.
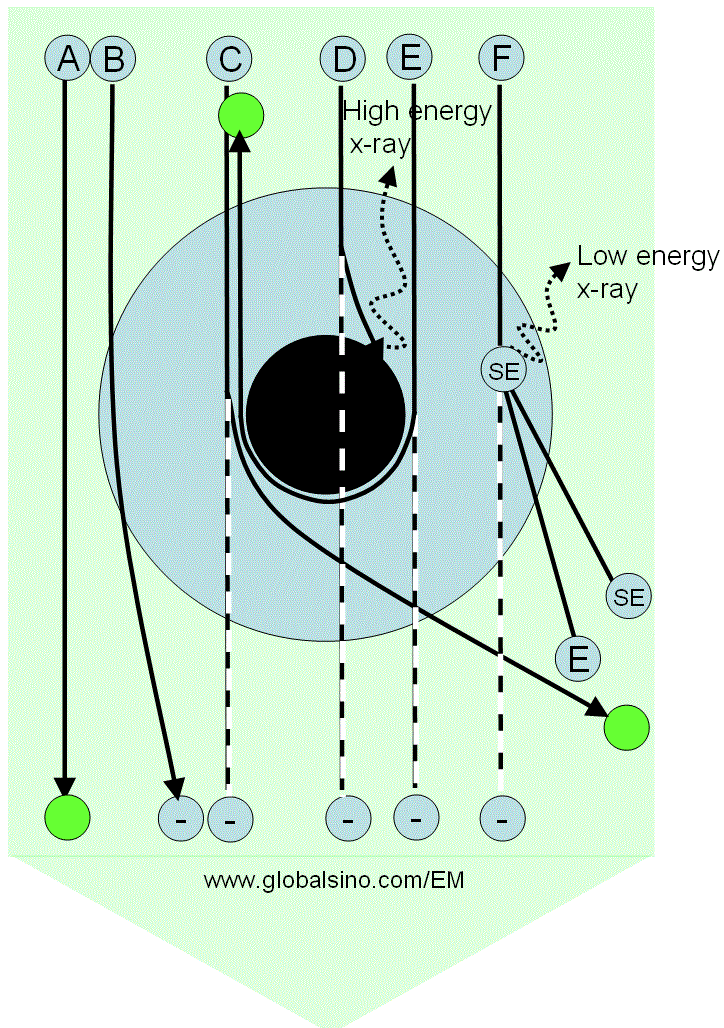
Figure 3768b. Possible interaction processes between the incident electrons and an atom. The large blue annular ring represents the electron cloud of the atom, while the black disk at the center represents the nucleus of the atom. The large green arrow represents the electron beam, while the letters A to F represent some rays in the electron beam. The green circles represent the electrons which do not lose energy after transmitting through the atom, while the circles labeled with a negative sign "− " indicates
missing intensity in the transmitted beam.
|
Table 3768c. Electron ray interaction with the atom. |
Electron ray |
Interaction and products |
A |
Does not interact with the sample |
B |
Is elastically scattered by the Coulomb force, induces a phase shift to the electron wave (resulting in diffraction contrast), and can be removed from the transmitted beam if the angle deviation is large |
C |
Is heavily scattered and removed from the transmitted beam. This scattering is very weak for light atoms such as C, N and H. |
D |
Is absorbed by the nucleus, producing X-rays at maximum energy, and the electrons are removed
from the transmitted beam, but it occurs rarely. This scattering is very weak for light atoms such as C, N and H. |
E |
Is the most heavily elastically scattered (backscattering electrons, BSEs) and removed from the transmitted beam |
F |
Collides with a shell electron, and thus inelastic scattering occurs. The ray can be removed from the transmitted beam if the deviation angle is large. In this case, both the energies of the scattered electron and secondary electrons are lower than that of the incident electrons. |
A semi-empirical model of electron scattering in solids was proposed by Kanaya and Okayama [1]. In the model, the incident
electrons suffer energy loss
due to collisions with the atomic electrons and to be deflected due to collisions with
the atomic nuclei in the specimen as shown in Figure 3768b. The cross-sections of the total electronic collision, including elastic nuclear and inelastic collisions, between the incident electrons and atoms can be given by a power potential,
V(r) =Ze2as-2/srs ----------------------------------------- [3768a]
with,
a=0.8853aHZ-1/3 ----------------------------------------- [3768b]
where,
Z -- the atomic number of the target,
e -- the electronic charge,
a -- the effective screened radius of the atom,
aH -- the Bohr radius of the hydrogen atom,
s -- a numerical parameter: s = 1 corresponds to Rutherford scattering and s=2 to
dE/dx = constant.
The maximum penetration depth, which is defined as the maximum depth
at which the electrons slow down to rest, of the electron beam can then be given by,
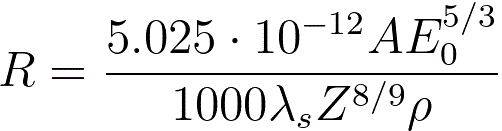
 --------------------------------------- [3768c]
where,
A -- the atomic weight [g/mol] of
the specimen material,
ρ -- the atomic density [kg/m3] of
the specimen material,
E0 -- the energy of incident electrons [eV],
λs -- (= 0.182) an empirical parameter.
The energy loss due to electronic collisions can be given by,
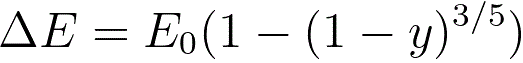
 --------------------------------------- [3768d]
where,
y -- the reduced depth (= z/R),
z -- the depth of the collisions.
Based on Figures 3768a and 3768b, the intensity of the incident electron beam, I0, can be given by,
I0 = I0·(ηB + ηA+ ηT) --------------------------------------- [3768e]
where,
ηB -- the fraction of the electrons backscattered in the layer of the specimen between the surface and depth z,
ηA -- the fraction of the electrons absorbed in the same layer,
ηT -- the fraction of the electrons transmitted into the forward hemisphere at depth z, which is given by,
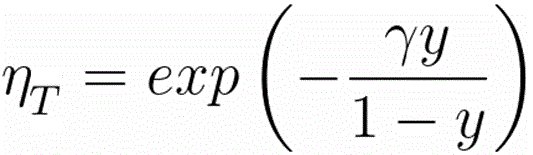
 ------------------------------------- [3768f]
where,
γ = = 0.187·Z2/3
[1] K. Kanaya and S. Okayama, Penetration and energy-loss theory of
electrons in solid targets, J. Phys. D. 5, 43 (1972).
|
