=================================================================================
In the formation of TEM diffraction patterns as shown in Figure 2682, the reciprocal lattice spacing Rhkl, measured as the distance from the origin (O, the location of the directly transmitted beam on the screen) to some diffraction spot (A), is related to the real crystal spacing dhkl, by,
dhkl =λL/Rhkl -------------------------------- [2682]
where,
L -- The camera length,
λ-- The wavelength of the incident electron beam,
λL -- The camera constant.
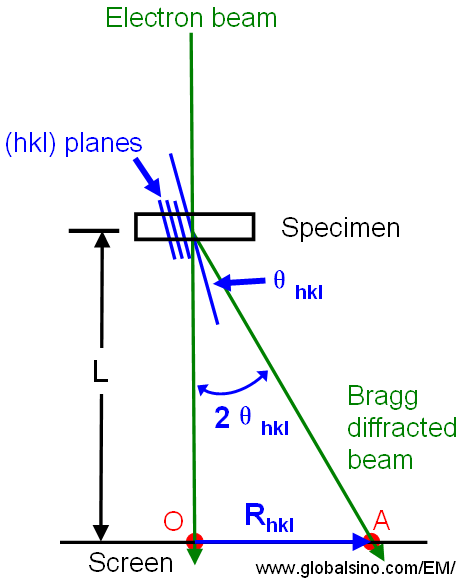
Figure 2682. The relationship between the reciprocal lattice spacing Rhkl and the camera length L for diffraction in a TEM.
In general, we can still obtain the d-spacings of the diffracting planes using Equation 2682 even though we don’t know the crystal structure. On the other hand, from Equation 2682, we can know that the ratio of any two R values gives the inverse ratio of the d-spacings.
Table 2682a shows the d-ratios for cubic crystal, where d1 and d2 are d-spacings.
Table 2682a. d-ratio for cubic crystal
d1/d2 |
100 |
110 |
111 |
200 |
211 |
220 |
311 |
100 |
1 |
|
|
|
|
|
|
110 |
1.414 |
1 |
|
|
|
|
|
111 |
1.732 |
1.225 |
1 |
|
|
|
|
220 |
2 |
1.414 |
1.155 |
1 |
|
|
|
211 |
2.45 |
1.732 |
1.414 |
1.225 |
1 |
|
|
220 |
2.828 |
2 |
1.633 |
1.414 |
1.155 |
1 |
|
311 |
3.32 |
2.345 |
1.915 |
1.658 |
1.354 |
1.173 |
1 |
Table 2682b. Excel files for calculations of lattice spacings and diffraction angles.
Due to the inaccuracy of eye judgment and/or the error from the digitalized user interface (UI) of the microscope software, to obtain the highest precision in quantifying spot spacings of crystals, we normally measure a distance between higher order spots, and then divide it by n+1 (here, n is the number of spots between the two higher order spots). However, this method can induce errors if the Ewald sphere cuts the spot at an angle, or if there is a slight distortion of the diffraction pattern caused by the projector lens of the microscope. Therefore, it is important to know the systematic errors of the TEM and software by measuring diffraction patterns of “ideal” crystals.
Note that the d-spacing and the intensities of the diffracted spots can be different for different crystals even though their space group are the same, for instance, as discussed in page3013 for space group Pnma (62).
|
