=================================================================================
In EMs, the kinetic energy (eV) gained by an electron as it is accelerated in the electron gun is equal to the electron's drop in potential energy (V0). Therefore, we have,
eV0 = m0v2/2 ---------------------------------- [4787a]
where,
v -- The electron velocity,
m0 -- The electron rest mass.
Based on Newtonian theory, the relation between the wavelength (λ) of a particle (e.g. electron here), moving at a velocity, v, is given by the de Broglie wave equation:
λ = h/m0v ---------------------------------- [4787b.a]
= h/(2m0eV0)1/2 ---------------------------------- [4787b.b]
where,
h -- The Planck's constant.
Because the accelerated electrons have a speed of approximately light speed (c), they should be treated using relativistic quantum mechanics, which are important in electron microscopy since the electrons are typically accelerated to potentials of 30 to 400 keV (about half the speed of light). By introducing the correction for relativistic effects, the wavelength is given by,
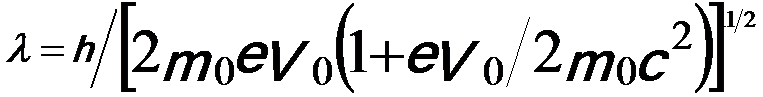 -----------------------------[4787c] -----------------------------[4787c]
The wavelength of the electrons is dramatically decreased with increase of the acceleration voltage; therefore, the spatial resolution of the microscopes is significantly improved. Note that, in electron microscopy it is normally sufficient only to replace the mass and wavelength of the electrons with the corresponding relativistic values [1]. Therefore, the relation between λ and V0 can be given by,
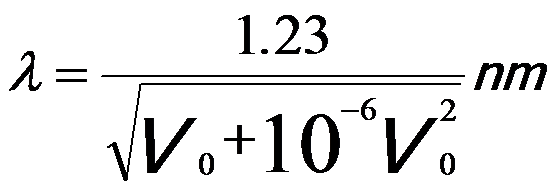 -----------------------------[4787d] -----------------------------[4787d]
Based on Equation 4787d, the wavelength can be obtained with the DM script . Table 4787 also lists the wavelength of incident electrons at commonly used accelerating voltages.
Table 4787. Wavelength of incident electrons at commonly used accelerating voltages.
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
400,000 |
0.00164366 |
|
|
500,000 |
0.00142028 |
|
|
|
|
|
|
Based on Equation 4787d, Figure 4787a gives the plot of relationship between wavelength and high voltage used in electron microscopes. We can see the voltage used in SEM and dual beam (Strata) systems is normally much lower than that used in TEM and STEM systems.
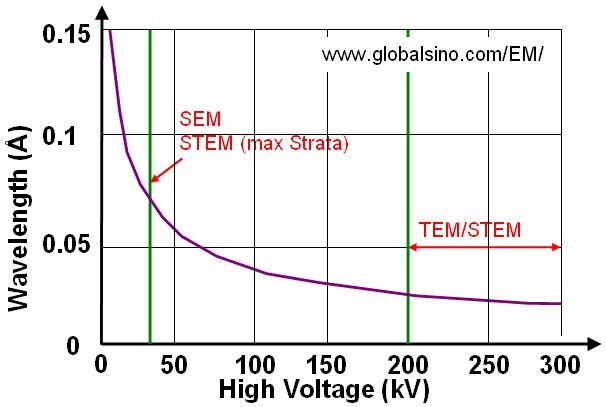 |
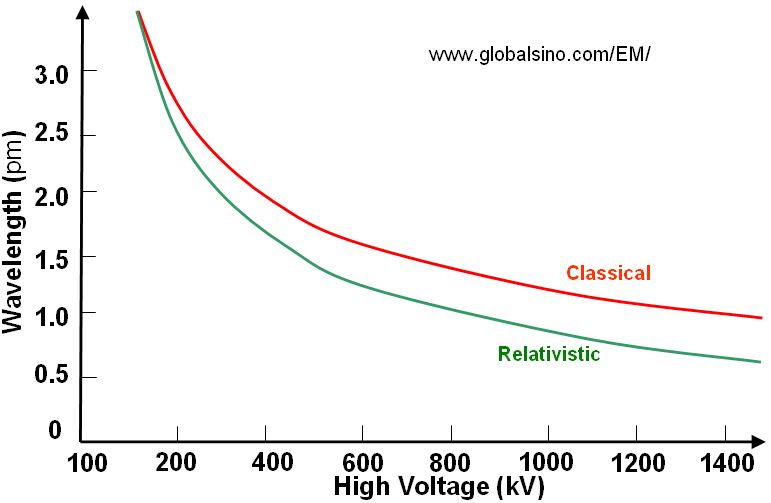 |
(a) |
(b) |
Figure 4787a. Plot of relationship between wavelength and high voltage.
Figure 4787b shows the wavelengths of gamma ray, x-ray, ultraviolet, visible light, near infrared, far infrared, microwave, radio, and incident electrons in electron microscopes.
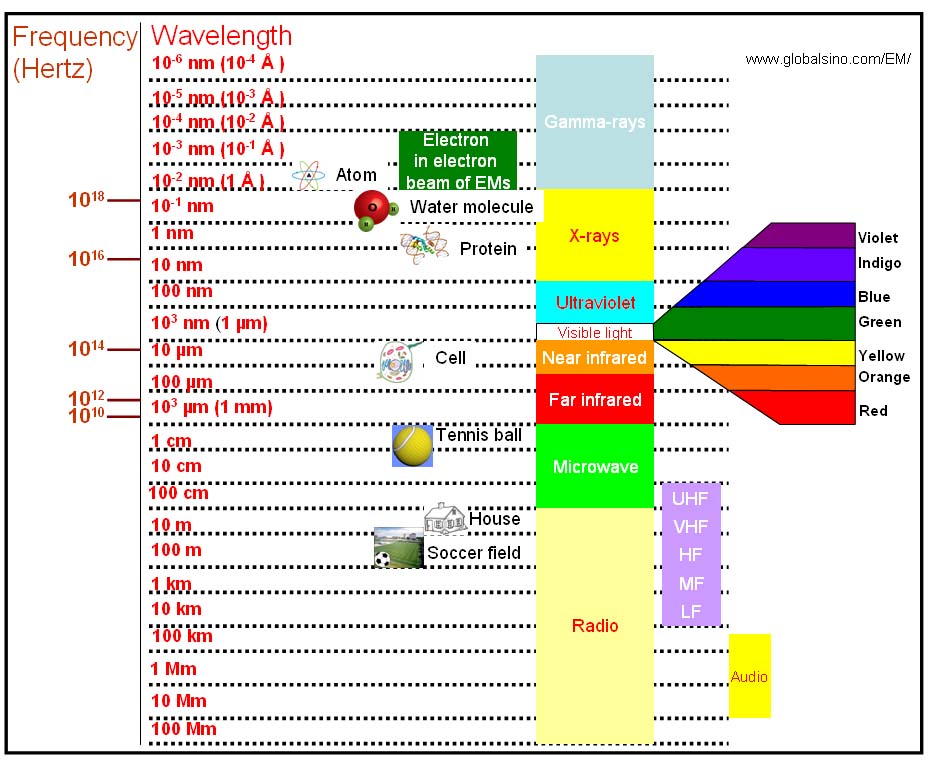
Figure 4787b. Various wavelengths of lights, microwave, radio, and incident electrons in EMs.
We can also calculate the electron velocities at different accelerating voltages, based on both Newtonian and Einsteinian theories, using Calculator 4787 below.
Calculator 4787. Electron velocities at different accelerating voltages.
[1] M. De Graef. Introduction to conventional transmission electron microscopy. Cambridge University Press,
2003.
|