=================================================================================
Optical aberration can be described by the so-called wave aberration function. For the ideal cases without aberrations, when an object is imaged using a perfect lens the wave at the back focal plane of a lens is spherical and is converged in the image plane (Ig, or called Ik for expression convenience). In actual lenses as shown in Figure 3752a, the wave aberration function is defined as the phase difference (χx,y) or the distance difference (Wx,y) in the optical path from the perfect (reference) spherical wave to the actual wavefront for the given lens. Since the area on the sample that is viewed at most of the time in EMs (especially in TEMs) is very small the wave aberration function’s dependence on the location of the point source in the object plane can be usually ignored, which is known as the isoplanatic approximation. The relationship between the phase difference (χx,y) and the distance difference (Wx,y) can be given by,
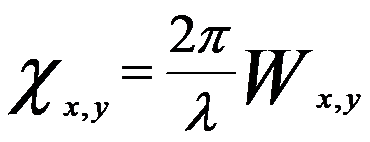 ------------------------- [3752a] ------------------------- [3752a]
where ,
λ -- The wavelength of the electron wave
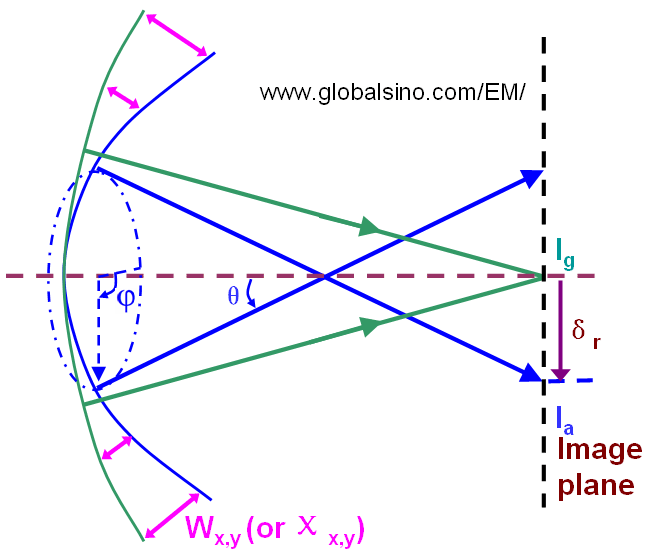
Figure 3752a. Schematic illustration of wave aberration function (Wx,y or χx,y) and ray aberration (δr).
In some cases for the convenience of theoretical expressions, the wave aberration function is simply given by the distance between the intersecting points (on the image plane) of the ideal ray and the aberrated ray indicated in in Figure 3752a. The distance (also called ray aberration), δr is given by,
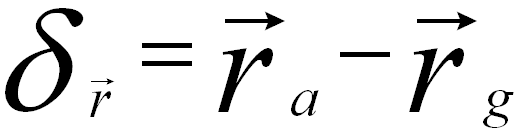 ------------------------- [3752b] ------------------------- [3752b]
The ray aberration is proportional to the gradient of the wave aberration Wx,y.
In general, the wave aberration function is determined by the following factors:
i) The complex reciprocal space vector k = kx + i ky.
ii) The position in the image plane r.
However, in the case of small field of view (e.g. at high magnifications), the dependence of Wx,y on the image plane can be negligible based on the isoplanatic approximation. The dependence of Wx,y on the image plane can also be neglected in STEM mode because of the small probe dimensions.
iii) The energy of the electrons (E0).
However, for a well-aligned field emission electron source, based on the monochromatic approximation the energy-dependent terms can be ignored.
In polar coordinate system, this two-dimensional (2-D) surface can be expressed as a function of the angle to the optic axis (θ) and azimuthal angle around the optic axis (ϕ) as shown in Figure 3752a. For a perfect lens, the actual wavefront is the same as the perfect spherical wavefront and χ(θ, ϕ) would be zero everywhere, but for a practical lens the actual wavefront is a function that is close to zero near the optical axis when a microscope is in the well-aligned (best imaging) condition and it increases rapidly when the high-order aberrations become predominant away from the optical axis. Furthermore, as shown in Figure 3752b the aberrated wavefront can be irregular so that the aberrations can be more complex and the wave aberration function can be both positive and negative.
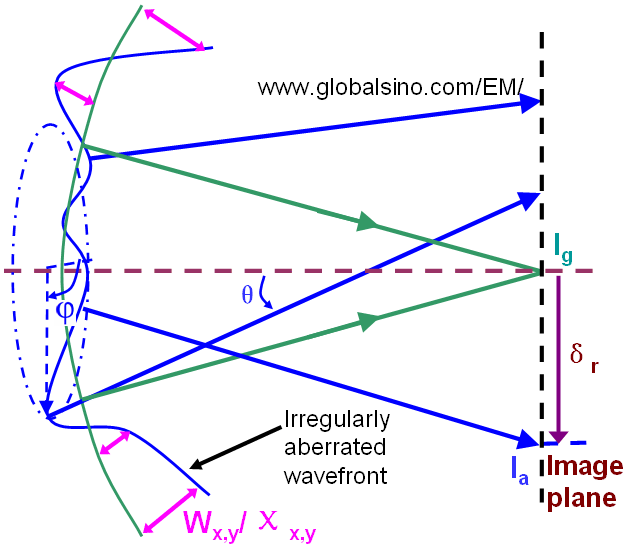
Figure 3752b. Schematic illustration of irregularly aberrated wavefront.
Note that the aberration behavior is described as a first-order aberration if the image aberration for defocus is linear in angle, while it is described as a third-order aberration if the image aberration for spherical aberration is cubic in angle. Optical aberrations negatively affect the image quality, imaging system transfer characteristics, and reduce precision of the relevant measurements. However, the key electron optical component affecting the formation of the images in CTEM and STEM is the objective lens so that in many cases we only need to consider the wave aberration function in the objective lens.
In practice, the imaging conditions in EMs are that the lens aberrations tend to zero for rays very close to the optic axis. In most cases, only the two lowest order terms of the wave aberration function (i.e., defocus (C1,0 or C1) and spherical aberration coefficients (C3,0 or C3)) are considered with the expression below,
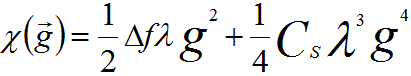 --------------------------------------- [3752c] --------------------------------------- [3752c]
where,
Δf -- The defocus, or C1,0 (or C1) with the notation of aberration coefficients in page3740.
CS -- The third-order spherical aberration coefficient C3,0 (or C3) in page3740.
g -- The spatial frequency.
λ -- The wavelength of incident electrons.
The phase-contrast term -isin2πχ(g) in the contrast transfer function becomes zero if CS=0 and Δf=0, while the amplitude-contrast term cos2πχ(g) is maximum, 1. Therefore, for aberration-corrected microscope, the TEM images present atomic structures by amplitude-contrast rather than by phase-contrast, and thus in HRTEM images the projected atom column are imaged in bright contrast on a dark background.
More comprehensively, under the isoplanatic approximation as well as Taylor expansion, the wave aberration function, W, using the notation provided by Krivanek [2], can be concisely expanded to sixth order in k about the origin of zero scattering angle in terms of the coherent aberration coefficients, given by,
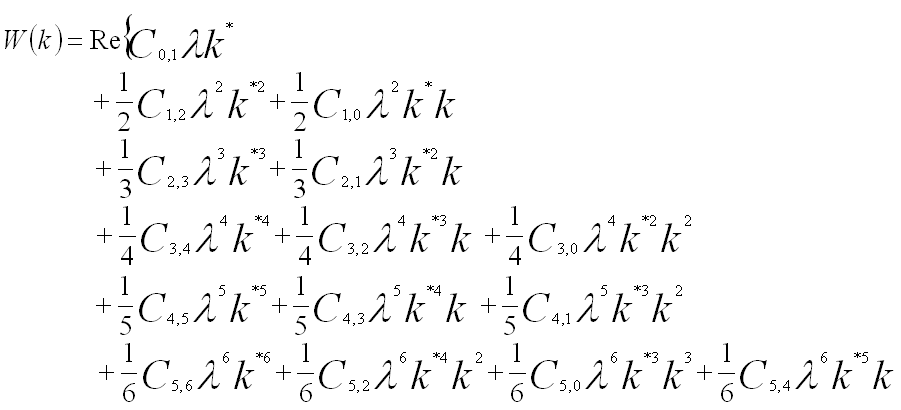
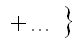 ----------------------------------------------- [3752d] ----------------------------------------------- [3752d]
Here, factors 1/(n+1) are used for all contributions to the nth order. [3] The first subscript refers to the order of the coefficient in terms of real space displacement, while the second subscript describes the angular symmetry. If the vector k is replaced by a complex angle variable ω = α·eiθ = ωx + iωy= λ(kx + iky), the wave aberration function can be re-writen by,
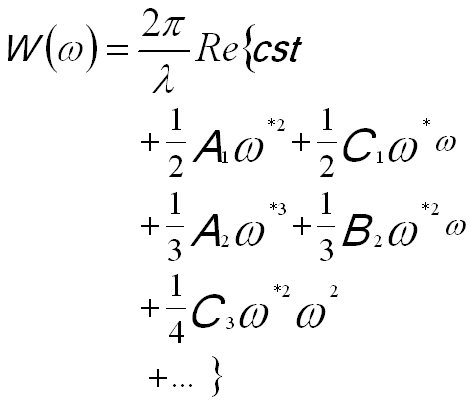 -------------------------------- [3752e] -------------------------------- [3752e]
or in a different format of,
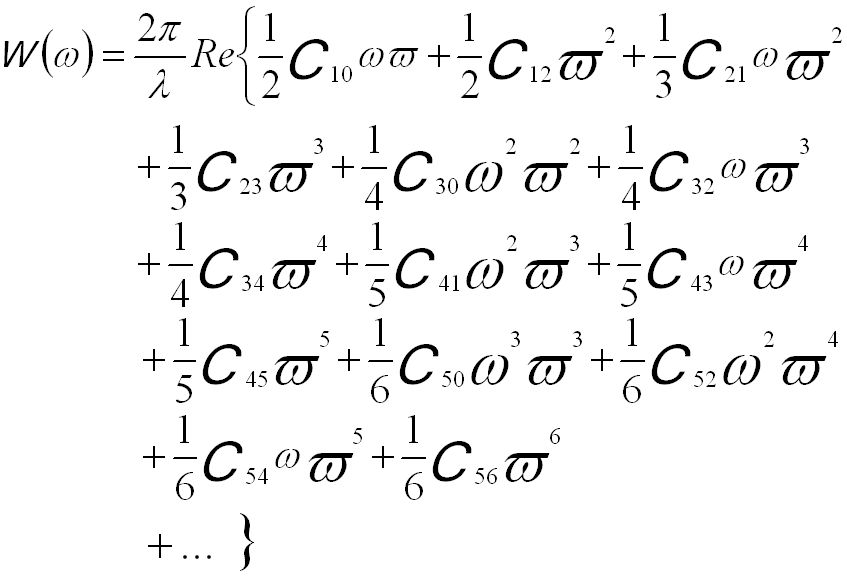 -------------------------------- [3752f.a] -------------------------------- [3752f.a]
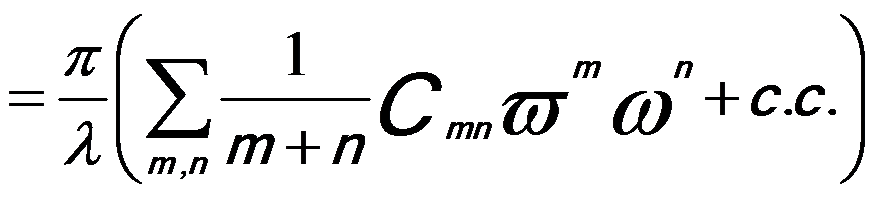 -------------------------------- [3752f.b] -------------------------------- [3752f.b]
where,
ω -- (= λg) the related complex scattering angle,
ϖ -- The complex conjugate of ω,
c.c. -- A complex conjugate.
ω = α·eiθ represents that the incident
ray has a tilt angle α and azimuth θ.
The wave aberration function can also be expanded in polar notation. The following equation shows the terms to fourth order,
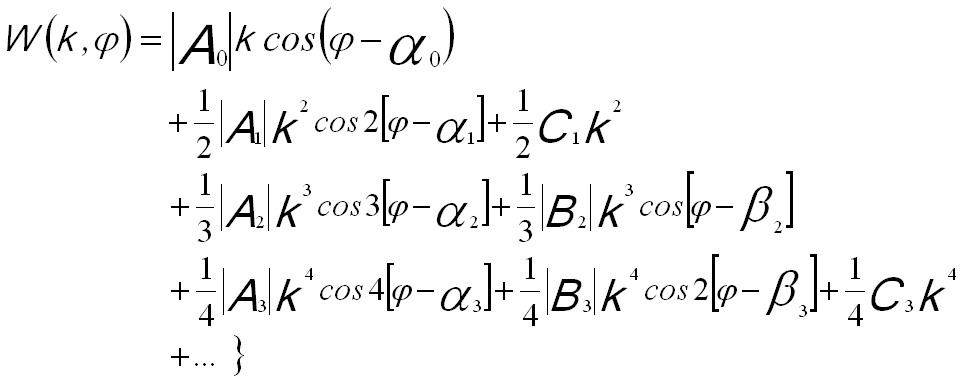 ----------- [3752g] ----------- [3752g]
The other way of presenting the wave aberration function is based on polar angular coordinates θ and φ, given by,
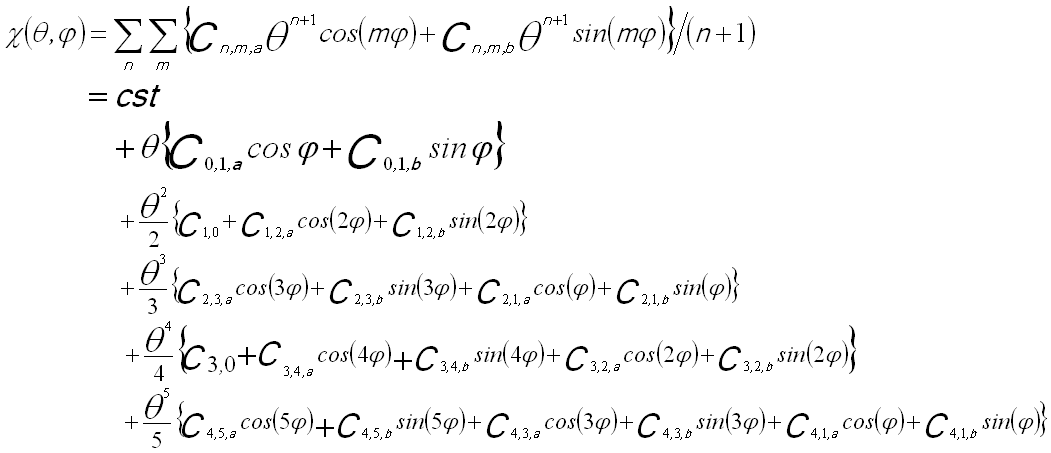
 --------------------------------------- [3752h] --------------------------------------- [3752h]
The sum over m is taken from 0 (or 1) to n+1 for each order n with the additional constraint that m+n is odd.
The wave aberration function can also be given as a function of scattering angle of the incident electrons and defocus of the objective lens, [2]
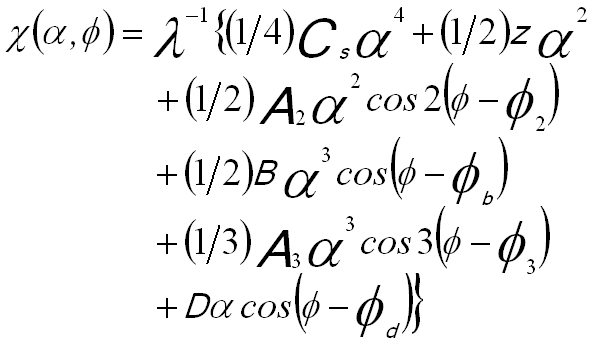 --------------- [3752i] --------------- [3752i]
where,
α -- The scattering angle,
z -- The defocus (the difference of TEM specimen height from the standard focus height),
A2 -- The two-fold astigmatism coefficients,
A3 -- The three-fold astigmatism coefficients,
B -- The coefficients corresponding to coma displacement,
D -- The coefficients corresponding to image displacement,
Φ2, Φb, Φ3 and Φd -- The initial phases of corresponding aberrations.
Table 3740 lists the aberration coefficient nomenclature, their order (of both the ray deviation (N) and the wavefront), and radial (azimuthal) symmetry.
The wave
front deviation due to the phase shift between the
wave function in the object plane ψobj(g) and the wave
function in the image plane ψim(g) is given by,
ψim(g) = ψobj(g)exp(-2πiχ(g)) ---------------------- [3752j]
The ray aberration is linked to the wave aberration by, [4]
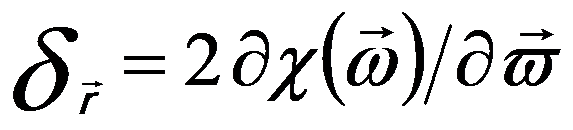 ---------------------- [3752k] ---------------------- [3752k]
For perfect aberration correction, because the aberration function is zero, all the ray displacements are eliminated, resulting in a zero contrast delocalization.
The wave aberrations (χ) produce a scrambling of amplitude and phase information in the EM (electron microscopy) images. Figure 3752c shows the schematic illustration of the image of a weak object formed by the objective lens. Sin(χ) indicates the cross-talk between amplitude and phase and cos(χ) presents the direct transfer of amplitude or phase information. For instance, in the conventional TEM, the detector only records the image amplitude, while in holography, both the amplitude and phase of the image wave are recorded in the interference fringes of the hologram.
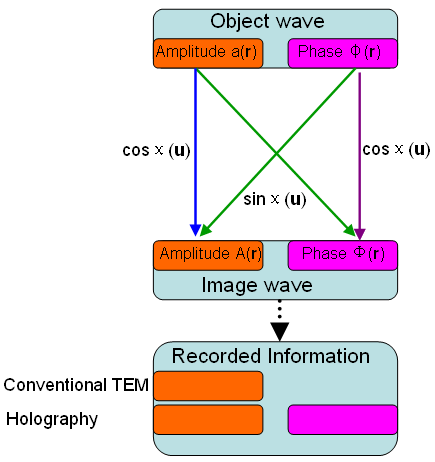
Figure 3752c. Schematic illustration of imaging a weak object. χ represents coherent wave aberration.
Furthermore, a small misalignment of the direction of the incident electron beam introduces wave aberrations and thus affects the quality of the images [ 5,6] so that coma-free alignment is essential for HRTEM.
[1] Hawkes, P., and Kasper, E. (eds.). (1996). “Principles of Electron Optics: Wave Optics.” Academic Press, London.
[2] K. Ishizuka, Ultramicroscopy 55 (1994) 407.
[3] Saxton,W.O. (2000). A new way of measuring microscope aberrations. Ultramicroscopy 81, 41–45.
[4] Lichte, H. (1991). Optimum focus for taking electron holograms. Ultramicroscopy 38, 13–22.
[5] K. Ishizuka and S. Iijima, Proc. 39th EMSA Annual Meeting,
Atlanta (1981) 96.
[6] D.J. Smith. W.O. Saxton, M.A. O’Keefe, G.J. Wood and
W.M. Stobbs. Ultramicroscopy I1 (1983) 263.
|
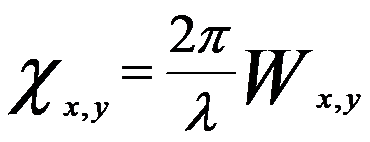 ------------------------- [3752a]
------------------------- [3752a] 

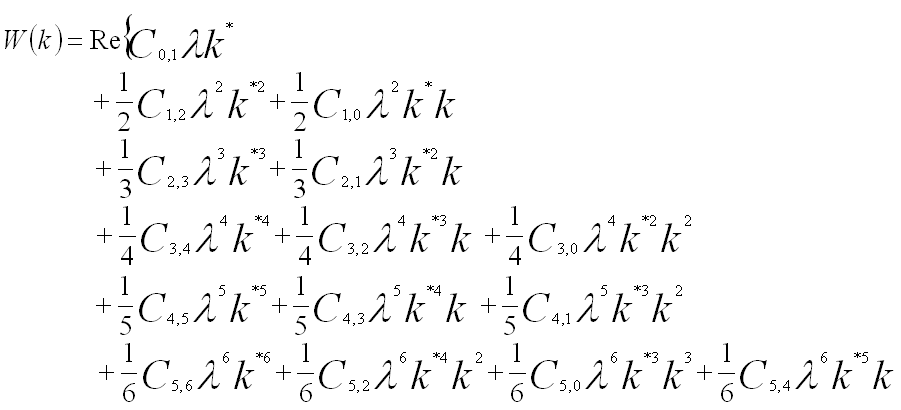
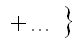 ----------------------------------------------- [3752d]
----------------------------------------------- [3752d]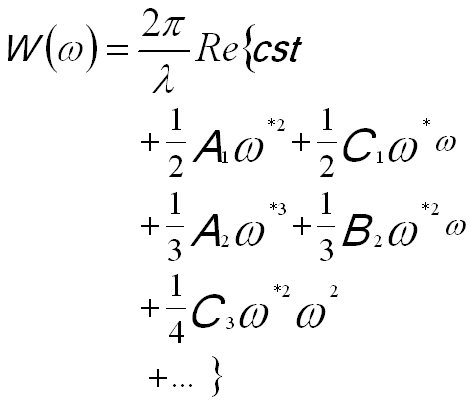 -------------------------------- [3752e]
-------------------------------- [3752e]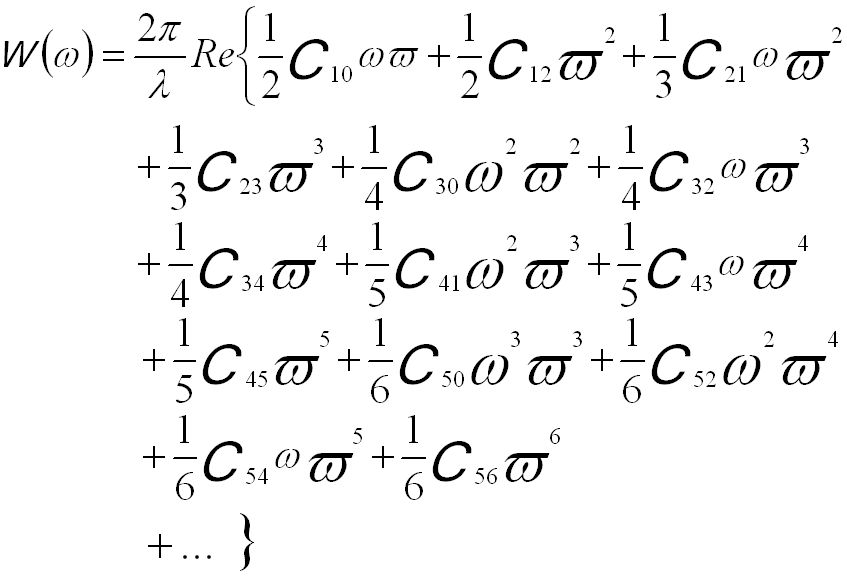 -------------------------------- [3752f.a]
-------------------------------- [3752f.a]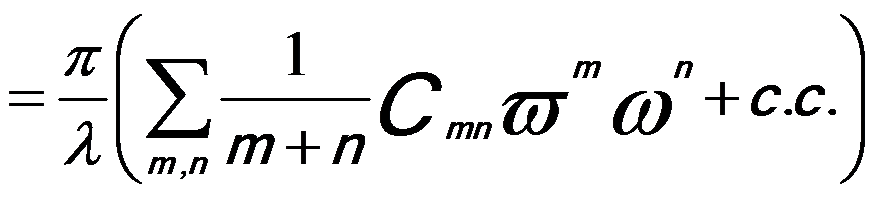 -------------------------------- [3752f.b]
-------------------------------- [3752f.b]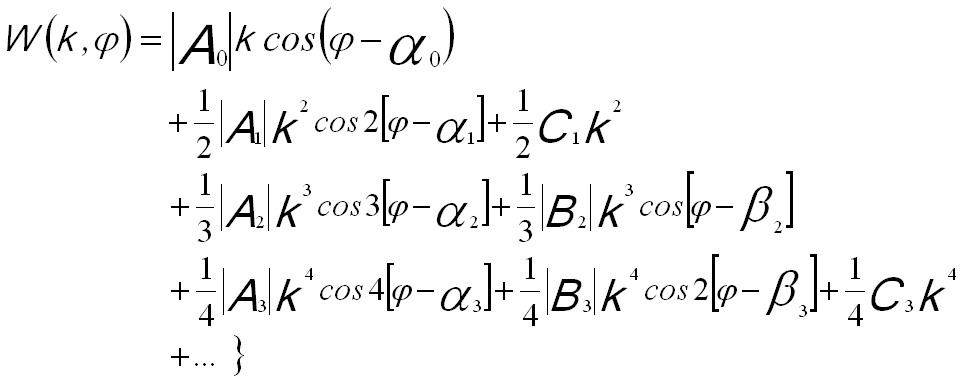 ----------- [3752g]
----------- [3752g]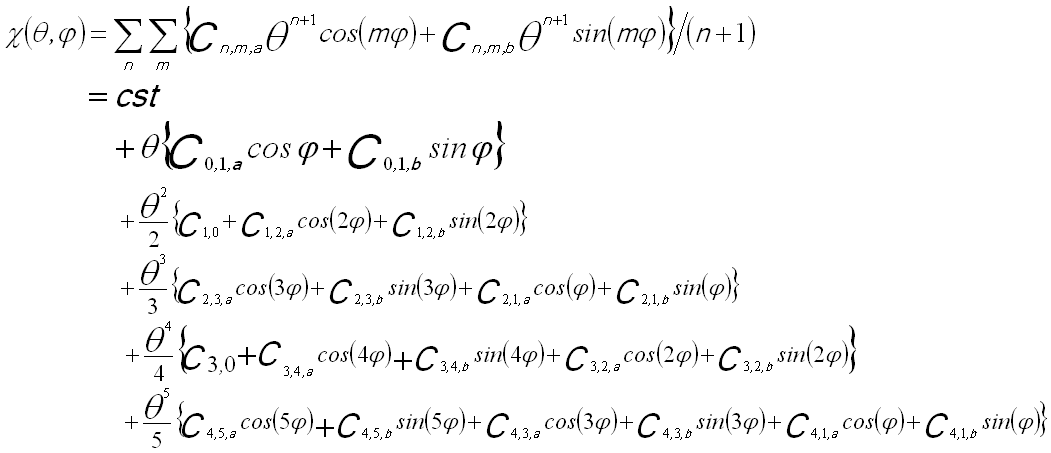
 --------------------------------------- [3752h]
--------------------------------------- [3752h]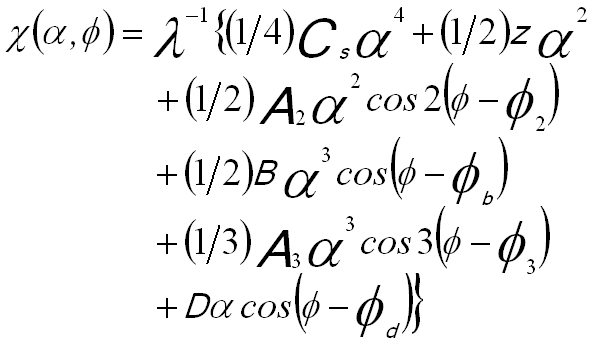 --------------- [3752i]
--------------- [3752i]