=================================================================================
In the classic diffraction theory, Bragg diffraction occurs when charged particle or electromagnetic radiation waves with a wavelength comparable to atomic spacing are incident to a crystalline sample. The waves reflected off adjacent scattering centers must have a path difference equal to an integral number of wavelengths. The scattered waves interfere constructively if they remain in phase. Therefore, the path difference between electron waves reflected from the upper and lower planes in Figure 3882 is equal to the total length (AO+BO). Assuming the hkl planes are spaced a distance dhkl apart and the wave is incident and reflected at angles θB, both AB and BC are equal to dsin(θB) and the total path difference should be equal to 2dsin(θB).
As discussed in page2678, we can have,
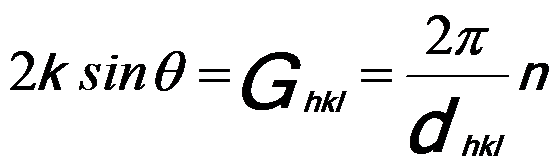 ------------------------------------------ [3882a] ------------------------------------------ [3882a]
where,
n -- The integer multiple
of the smallest
Ghkl that is allowed,
k = 2π/λ.
Therefore, we can obtain the well-known Bragg’s diffraction condition, given by,
nλ = 2dhklsin(θB) -------------------------------------------- [3882b]
where,
n -- An integer, the order of reflection;
dhkl -- The lattice spacing of (hkl);
λ -- The wavelength of the charged particle or electromagnetic radiation waves;
θB -- The Bragg angle that is the
angle between the incident wave vector and the
lattice planes as shown in Figure 3882,
hkl -- Miller indices.
The Bragg angle θB is a very important concept in diffraction theory, e.g. widely used to explain electron and X-ray diffraction phenomena. Very strong intensities known as Bragg peaks are obtained in the diffraction pattern when scattered waves satisfy the Bragg condition. The angle between incident and reflected waves is equal to 2θB as shown in Figure 3882.
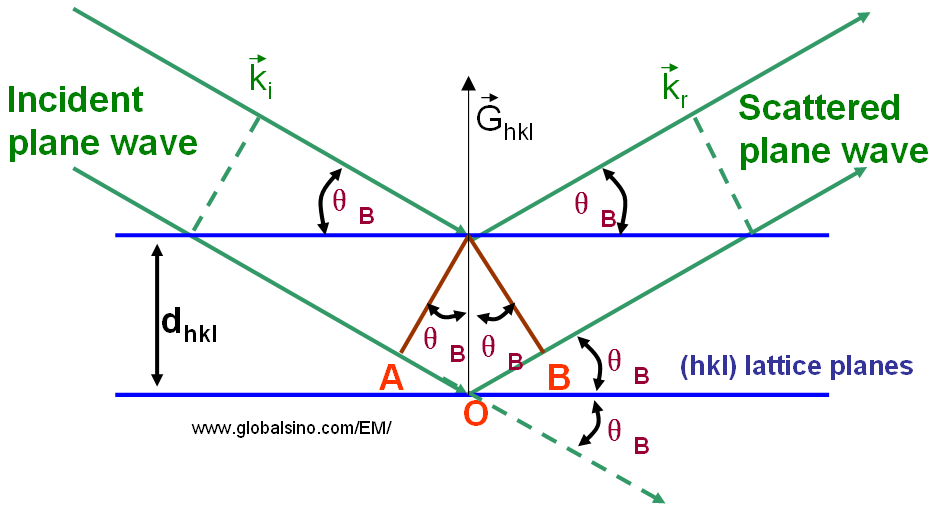
Figure 3882. Schematic illustration of Bragg condition and Bragg’s law.
The path difference between reflected waves is equal to AO + BO.
For FCC and BCC structures, the lattice constants are given by, (You can download the excel file for your own calculations)
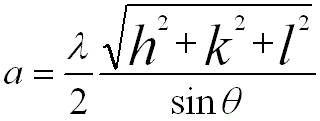 ----------------- [3882c] ----------------- [3882c]
Table 3882a shows that electrons interact with 1 electron, many electrons, 1 nucleus, and many nuclei in solids.
Table 3882a. Effects of interactions of electrons in solids.
| |
Interaction with electron(s) |
Interaction with nucleus/nuclei |
| |
1 electron |
Many electrons |
1 nucleus |
Many nuclei |
| Scattering type |
Inelastic |
Inelastic |
Quasi-elastic |
Elastic |
Inelastic |
| Scattering effect |
Electron Compton effect; electron excitation (from 50 eV to a few keV: EDS and EELS) |
Plasmon excitation (< 50 eV, ~100 nm TEM specimen); Cerenkov effect |
Rutherford scattering; phonon scattering (< 1 eV, heat) |
Bragg scattering |
Bremsstrahlung |
Table 3882b lists some examples of Bragg angles at various beam voltages for typical d-spacing. The Bragg angles were obtained with Equation 3882b (for n = 1).
Table 3882b. Bragg angles at various beam voltages for typical d-spacing.
| Accelerating voltage (kV) |
Wavelength (nm) |
Crystals |
d-spacing (nm) |
Bragg angle (° & mrad) |
| 100 |
0.0037 |
Typical biological crystals |
10 |
0.0106° (0.19 mrad) |
| 200 |
0.0025 |
Nickel (Ni) |
0.203 |
0.353° (6.16 mrad) |
In actual experiments, different from diffuse scattering, the Bragg peaks come from the long-range ordered structure. Crystalline specimens have to be tilted in a goniometer in TEM in order to:
i) Observe lattice fringes and crystal structures.
ii) Determine the crystal orientation.
iii) Observe diffraction contrast of lattice defects with certain Bragg reflections or known orientation.
iv) Determine the Burgers vector of lattice defects.
Table 3882c. Digital Micrograph scripts to compute reflection angles of crystals.
|
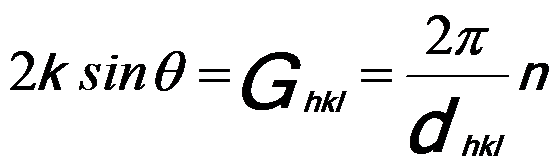 ------------------------------------------ [3882a]
------------------------------------------ [3882a]