=================================================================================
In images formed by elastic scattering (e.g. HRTEM images), contrast delocalization is referred to as the loss of image contrast due to lens aberrations or called blurring effect. In this case, the image information is blurred and displaced from their true locations in the TEM specimen. In other words, the contrast delocalization can also be expressed as the lateral displacement of spatial frequencies in the image, and thus indicates the feature (e.g. the image of an atom) is displaced from its "true location" in the real object. This displacement increases with spatial frequency significantly. It is rarely a problem on the microscopes with LaB6 guns due to their limited coherence in illumination. However, it is a significant imaging artifact in HRTEM images taken from microscopes with field emission guns (FEGs) due to their high coherence that causes a strong contribution of the high spatial frequencies. This makes the image delocalization becomes more important and cannot be reduced to zero.
The origin of the contrast delocalization is the imaging of an object point P into an aberration disk of radius ΔR rather than into the ideal image point Pi. Mathematically, the contrast delocalization ΔR can be given by,
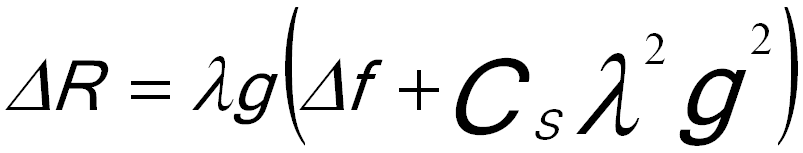 ---------------- [1715a] ---------------- [1715a]
where,
λ -- The electron wavelength,
g -- The spatial frequency,
Δf -- The defocus,
Cs -- The spherical aberration of the objective lens.
In other words, the delocalization of the image from its "true location" in the real object can be given by,
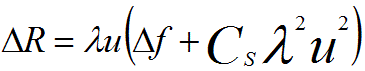 ---------------- [1715b] ---------------- [1715b]
where,
u -- The coordinates on the image of the spatial frequency.
Depending on the parameters in Equation 1715a, the contrast delocalization can extend up to a couple of nanometers. Furthermore, this blurring effect becomes significant at nonperiodic structures in materials, e.g. interfaces, boundaries, edges, and defects.
The optimal defocus for minimizing the delocalization ΔR is given by,
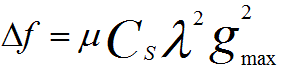 ---------------- [1715c] ---------------- [1715c]
where,
µ -- A constant which is between 0.75 and 1.
gmax -- The maximum spatial frequency which is determined by the information limit and is selected by a proper objective aperture.
Lichte defocus of least confusion minimizes contrast delocalization, however, the strong spherical aberration under this condition induces the poor point resolution and the contrast reversals in the entire frequency range. For a modern uncorrected 300-kV TEM with Cs = 0.6 mm and an information limit of 0.1 nm, the actual point resolution is only 0.17 nm and the smallest delocalization is up to even 1.2 nm! [1]
For perfect aberration correction, because the aberration function is zero, all the ray displacements are eliminated, resulting in a zero contrast delocalization.
If the spherical aberration (Cs) is zero in a Cs-corrected microscope, positive phase contrast of a weak-phase object can still be obtained by the defocus,
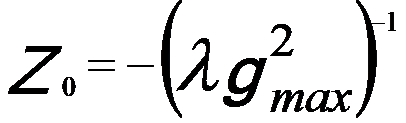 ----------------------------------- [1715d] ----------------------------------- [1715d]
This condition presents a pass band up to the information limit (gmax) at the contrast delocalization of R0 = 1/gmax.
Based on Cs correction, extending Scherzer’s point resolution to information limit of the microscope can also optimize the positive phase contrast from a weak-phase object. Assuming gSch = gmax and a defocus of ZSch = -8/(3λg2max)
, one can obtain, [2]
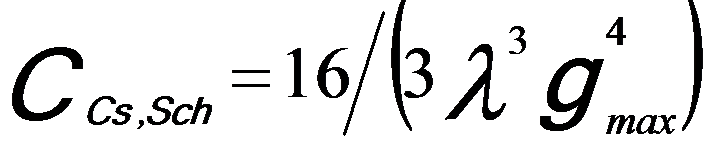 ---------------------- [1715e] ---------------------- [1715e]
The resulting contrast delocalization is given by,
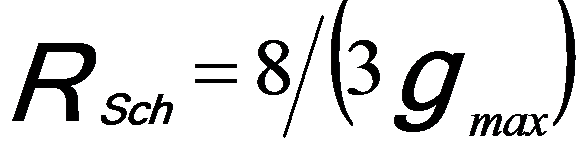 ---------------------- [1715f] ---------------------- [1715f]
In this case, the atoms are observed in dark contrast with respect to the background.
[1] Markus Lentzen, Progress in Aberration-Corrected High-Resolution
Transmission Electron Microscopy Using Hardware Aberration Correction, Microsc. Microanal. 12, 191–205, 2006.
[2] Lentzen, M., Jahnen, B., Jia, C.L., Thust, A., Tillmann, K. &
Urban, K. (2002). High-resolution imaging with an aberrationcorrected
transmission electron microscope. Ultramicroscopy
92, 233–242.
|
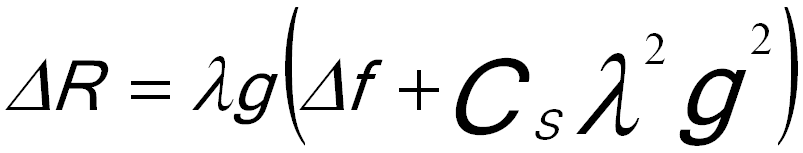 ---------------- [1715a]
---------------- [1715a] 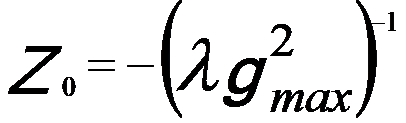 ----------------------------------- [1715d]
----------------------------------- [1715d]