=================================================================================
Third-order spherical aberration is one of the dominant geometric aberrations that limit the spatial resolution of EMs (electron microscopes). Figure 3654 shows the octupole design, normally used for spherical aberration (Cs) correction. The optical axis, along which the electrons travel, is into the page.  indicates the direction of the electron beam. The blue arrowed curves represent the magnetic field lines, while the red and plum arrowed lines represent the Lorentz force on the electrons. From Equation 4313, we can know the field in the octupole system can be given by, indicates the direction of the electron beam. The blue arrowed curves represent the magnetic field lines, while the red and plum arrowed lines represent the Lorentz force on the electrons. From Equation 4313, we can know the field in the octupole system can be given by,
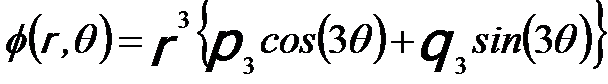 ---------------------------- [3654] ---------------------------- [3654]
Namely, it varies by r3, which acts directly as third order aberrations, increasing with distance from the optical axis. Note that multipoles of higher-order than 3 do not produce 3rd-order spherical aberrations at all.
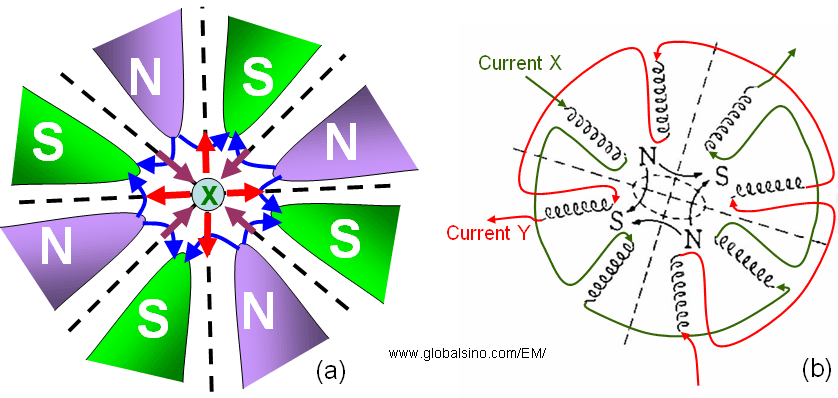
Figure 3654. The octupole design.
The plum
arrows show focusing
function, while the red arrows show defocusing function.
Table 3654 lists the aberration coefficient nomenclature, their order (of both the ray deviation (N) and the wavefront), and radial (azimuthal) symmetry, as well as highlights the third-order spherical aberration in blue. This table also compares both commonly used notations [1, 2].
Table 3654. Aberration Coefficient Nomenclature. The aberration coefficients have two
main types of notations, namely Krivanek notation, and Typke and Dierksen notation.
| Krivanek notation |
Typke and Dierksen notation |
Radial Order |
Azimuthal Symmetry |
Nomenclature |
| Ray |
Wave (k) |
| C0,1 |
A0 |
0 |
1 |
1 |
Image Shift |
| C1,2 |
A1 |
1 |
2 |
2 |
Two-fold axial astigmatism (or axial astigmatism of the 1st order) |
| C1,0 |
C1 |
1 |
2 |
0, ∞ |
Defocus (overfocus positive, or spherical aberration of the 1st order; Real numbers and describing rotationally symmetric contributions to the wave aberration) (alt: Δf) |
| C2,3 |
A2 |
2 |
3 |
3 |
Three-fold axial astigmatism (or axial astigmatism of the 2nd order)
|
| C2,1 |
B2 |
2 |
3 |
1 |
Axial coma |
| C3,4 |
A3 |
|
4 |
4 |
Four-fold axial astigmatism or axial astigmatism of the 3rd order Cs |
| C3,2 |
B3 |
|
4 |
2 |
Twofold astigmatism of Cs (or Third order twofold astigmatism, or Axial star aberration of the 3rd order) |
| C3,0 |
C3 |
|
4 |
0, ∞ |
Third-order spherical aberration (always positive for round lenses [3]; Real numbers and describing rotationally symmetric contributions to the wave aberration) (alt: Cs ) |
| C4,5 |
A4 |
|
5 |
5 |
Five-fold axial astigmatism or axial astigmatism of the 4th order |
| C4,1 |
B4 |
|
5 |
1 |
Fourth-order axial coma |
| C4,3 |
D4 |
4 |
5 |
3 |
Fourth order threefold astigmatism (or Three lobe aberration) |
| C5,6 |
A5 |
|
6 |
6 |
Six-fold axial astigmatism or sixfold axial astigmatism of the 5th order |
| C5,4 |
R5 |
5 |
6 |
4 |
Fourfold astigmatism of C5 (or Fifth order rosette aberration) |
| C5,2 |
S5 |
5 |
6 |
2 |
Twofold astigmatism of C5 (or Fifth-order axial star aberration) |
| C5,0 |
C5 |
|
6 |
0, ∞ |
Fifth-order spherical aberration |
| |
D5 |
|
|
|
Four lobe aberration of the 5th
order |
The 6-fold astigmatism (A6) generated by the first and second hexapoles in a Cs corrector can be cancelled out by the one from the combination of third-order aberrations of the transfer lenses and the 3-fold astigmatism introduced by the hexapole elements. [4]
[1] Krivanek, O. L., Dellby, N., and Lupini, A. R. (1999). Towards sub-Å electron beams.
Ultramicroscopy 78, 1.
[2] Typke, D., and Dierksen, K. (1995). Determination of image aberrations in high-resolution
electron microscopy using diffractogram and cross correlation methods. Optik 99, 155.
[3] O. Scherzer, J. Appl. Phys. 20 (1949) 20.
[4] Müller H, Uhlemann S, Hartel P, and Haider M (2006) Advancing the
hexapole Cs-corrector for the scanning transmission electron microscope.
Microsc. Microanal. 12: 442–455.
|
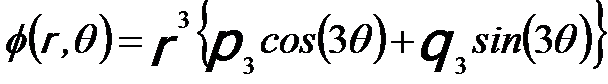 ---------------------------- [3654]
---------------------------- [3654] 