|
This book (Practical Electron Microscopy and Database) is a reference for TEM and SEM students, operators, engineers, technicians, managers, and researchers.
|
=================================================================================
So far only two types of aberration correctors have been proposed:
i) Conventional objective lens in combination with five multipole elements [2],
ii) Two hexapoles and four weak transfer lenses apart from the strong objective lens [3].
The second type has the advantage that the hexapole fields need only a stability of about 10 ppm, which is two orders of magnitude less than that required for the quadrupole fields of the multipole correctors, while it has the disadvantage that it cannot compensate for the chromatic aberration.
The first of Scherzer’s theorem suggested that the rotational symmetry from the round lenses induces unavoidable spherical aberrations (Cs). Therefore, to correct the Cs one way is to break the symmetry. This has been established by using electromagnetic multipole lenses such as 2 (dipole), 4 (quadrupole), 6 (sextupole), 8 (octupole) poles, and so on, alternating North and South around the optic axis.
Based on the Lorentz force solution from the given magnetic field of a multipole lens (2N poles) in free space, the electron trajectory can be extracted. Assuming that the magnetic poles have an ideal shape, the magnetic scalar potential obtained from the Laplace’s equation can be given by [1],
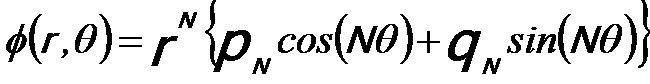 ----------------------- [4313] ----------------------- [4313]
where the r and θ are polar coordinates, for instance, shown in Figure 3661 for the dipole case. The similarity between Equations 3752f and 4313 indicates that the multipole lens can be used to correct the aberration in the conventional lenses. Based on this principle, multipole lens, especially quadrupole, can be used to directly correct simple astigmatism.
Note that in EMs except for alignment deflectors, stigmators, and multipole aberration correctors, all the other conventional optical lenses are cylinder symmetric.
[1] Jackson, J. D. (1999), Classical Electrodynamics, John Wiley & Sons Inc, New York.
[2] H. Rose, Elektronenoptische Aplanate, Optik 34 (1971) 285.
[3] Rose H. 1990. Outline of a spherically corrected semiaplanatic medium-voltage transmission electron-microscope. Optik 85:19–24
|