=================================================================================
Based on the Lorentz force solution from the given magnetic field of a multipole lens (2N poles) in free space, the electron trajectory can be extracted. Assuming that the magnetic poles have an ideal shape, the magnetic scalar potential obtained from the Laplace’s equation can be given by [1],
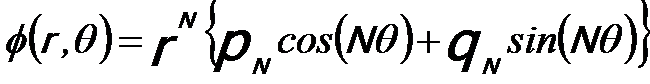 ----------------------- [3656] ----------------------- [3656]
where the r and θ are polar coordinates, for instance, shown in Figure 3661 for the dipole case. The similarity between Equations 3752f and 3656 indicates that the multipole lens can be used to correct the aberration in the conventional lenses. Based on this principle, multipole lens, especially quadrupole, can be used to directly correct simple astigmatism.
The two-fold astigmatism is the primary astigmatism of a TEM objective lens (OL). It often requires to be corrected during TEM operations. There are mainly three ways to correct the OL astigmatisms:
i) Using Fresnel fringes. This is the most usual way of correcting the OL astigmatisms. This method requires a small hole of a thin region in the sample. Its drawback is that it may not be able to apply to some materials, for instance, a slight position change (tilt or translation) of a magnetic sample can result in a huge change of the stigmatism.
ii) Based on diffractogram (Thon’scurve). This method requires an amorphous phase of a thin region in a sample. Similar to method i), the drawback of this method is that it may not be able to apply to some materials.
iii) Using the caustic image. The advantages of this method are: A) Applicable to any materials including magnetic/crystalline/thick materials, and B) Coma-free alignment can be performed at the same time.
Figure 3656 shows Thon rings with different image qualities.
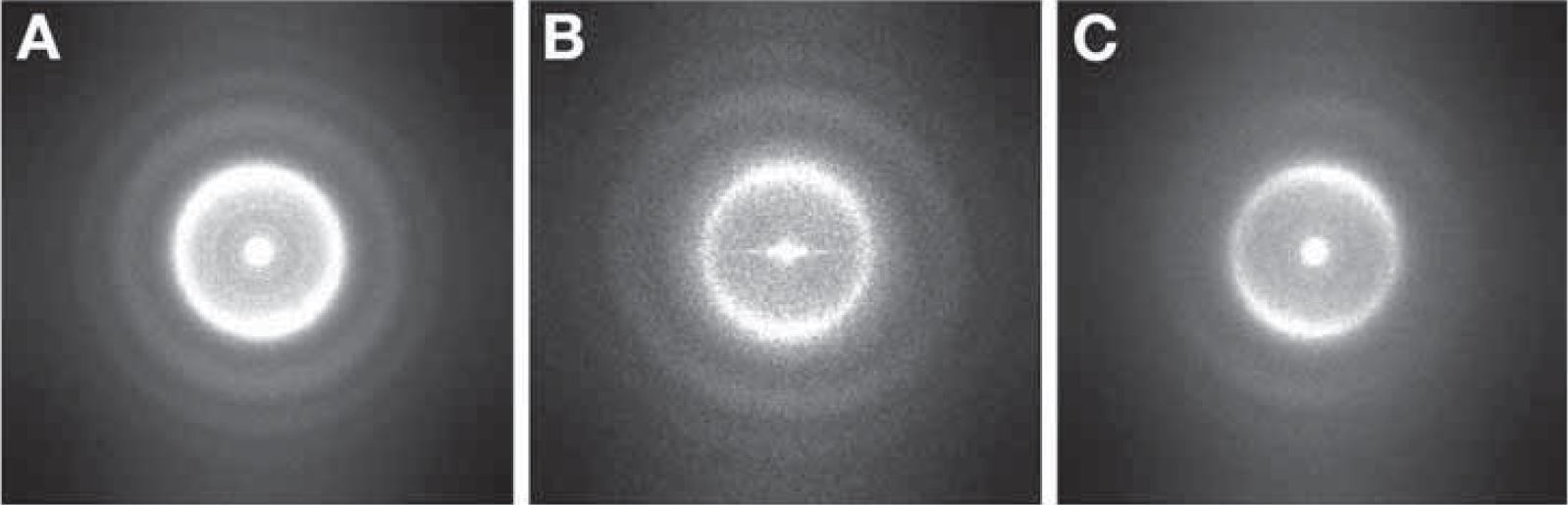
| Figure 3656. Thon rings with different image qualities: (A) good; (B) anisotropic due to astigmatic; (C) anisotropic due to specimen drift. [2] |
[1] Jackson, J. D. (1999), Classical Electrodynamics, John Wiley & Sons Inc, New York.
[2] Electron Microscopy: Methods and Protocols, Second Edition, 2007, Edited by John Kuo.
|