=================================================================================
In conventional high-resolution TEM, the fixed large value of the third-order spherical aberration imposes limit to the contrast transfer of thin objects. However, it is necessary to eliminate all the second-order aberrations (highlighted in light orange in Table 3618) before correcting the third-order aberrations (highlighted in green in Table 3618), since the second-order aberrations are larger than the third-order aberrations caused by the rotationally symmetric fields.
Table 3618. Aberration Coefficient Nomenclature. The aberration coefficients have two
main types of notations, namely Krivanek notation, and Typke and Dierksen notation.
| Krivanek notation |
Typke and Dierksen notation |
Radial Order |
Azimuthal Symmetry |
Nomenclature |
| Ray |
Wave (k) |
| C0,1 |
A0 |
0 |
1 |
1 |
Image Shift |
| C1,2 |
A1 |
1 |
2 |
2 |
Two-fold axial astigmatism (or axial astigmatism of the 1st order) |
| C1,0 |
C1 |
1 |
2 |
0, ∞ |
Defocus (overfocus positive, or spherical aberration of the 1st order; Real numbers and describing rotationally symmetric contributions to the wave aberration) (alt: Δf) |
| C2,3 |
A2 |
2 |
3 |
3 |
Three-fold axial astigmatism (or axial astigmatism of the 2nd order)
|
| C2,1 |
B2 |
2 |
3 |
1 |
Axial coma |
| C3,4 |
A3 |
|
4 |
4 |
Four-fold axial astigmatism or axial astigmatism of the 3rd order Cs |
| C3,2 |
B3 |
|
4 |
2 |
Twofold astigmatism of Cs (or Third order twofold astigmatism, or Axial star aberration of the 3rd order) |
| C3,0 |
C3 |
|
4 |
0, ∞ |
Third-order spherical aberration (always positive for round lenses [4]; Real numbers and describing rotationally symmetric contributions to the wave aberration) (alt: Cs ) |
| C4,5 |
A4 |
|
5 |
5 |
Five-fold axial astigmatism or axial astigmatism of the 4th order |
| C4,1 |
B4 |
|
5 |
1 |
Fourth-order axial coma |
| C4,3 |
D4 |
4 |
5 |
3 |
Fourth order threefold astigmatism (or Three lobe aberration) |
| C5,6 |
A5 |
|
6 |
6 |
Six-fold axial astigmatism or sixfold axial astigmatism of the 5th order |
| C5,4 |
R5 |
5 |
6 |
4 |
Fourfold astigmatism of C5 (or Fifth order rosette aberration) |
| C5,2 |
S5 |
5 |
6 |
2 |
Twofold astigmatism of C5 (or Fifth-order axial star aberration) |
| C5,0 |
C5 |
|
6 |
0, ∞ |
Fifth-order spherical aberration |
| |
D5 |
|
|
|
Four lobe aberration of the 5th
order |
The secondary effects of sextupoles produce spherically symmetric 3rd-order aberrations if paraxial optics is rotationally symmetric. These secondary aberrations depend quadratically on the sextupole strength. Therefore, magnetic hexapoles combined with transfer round lenses [1] are used for third-order spherical aberration correction at high accelerating voltages in TEM and STEM. However, the image quality can be improved by this correction only if the primary 2nd-order aberrations of the sextupoles are eliminated as well and if the 4th-order aberrations can be kept adequately small.
Figure 3618 shows the simplest system which can eliminate all second-order fundamental rays and thus all the second-order aberrations outside of the corrector. It consists of a round lens doublet and two identical sextupoles. The outer focal points of the corrector are the same as the nodal points N1 and N2 of the round lens doublet. The coils of the round lenses are connected oppositely in order to avoid an image rotation from the first sextupole, which is independent of the current strength. Therefore, the doublet images the front sextupole with magnification of −1 exactly onto the second sextupole centered about the nodal point N2 without introducing an off-axial third-order coma. This system can correct the third-order spherical aberrations of electron microscopes [2].
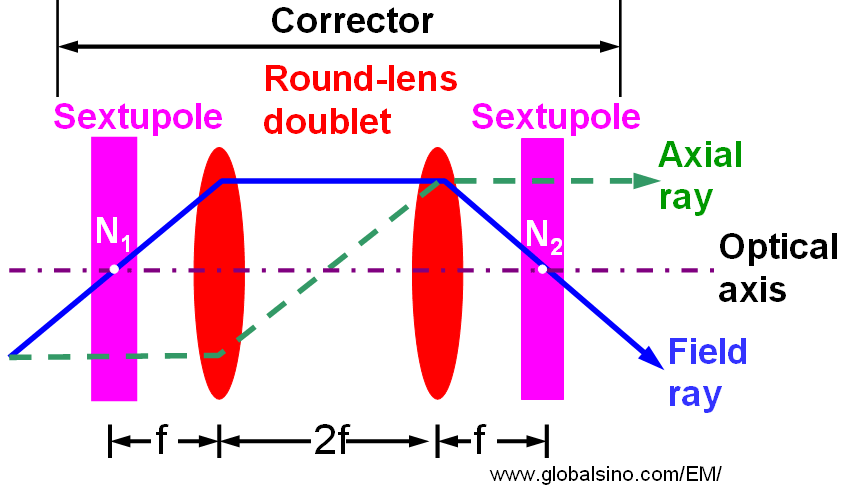
Figure 3618. Schematic illustration of a simplest spherical-aberration corrector. Adapted from [3].
Note that a single aberration violating the π/4 criterion may also cancel out the other one with the same symmetry if the have different sign, such as a small positive third-order spherical aberration and a small underfocus, or a small positive twofold astigmatism and a small negative third-order star aberration with the same azimuth.
[1] Haider, M., Braunshausen, G. and Schwan, E. 1995. Correction of the spherical aberration of a 200 kV TEM
by means of a hexapole-corrector, Optik, 99, 167–179.
[2] Born M. and Wolf E., 1975, Principles of Optics (Oxford:
Pergamon Press).
[3] Rose H. H., Optics of high-performance electron microscopes, Sci. Technol. Adv. Mater. 9 (2008) 014107.
[4] O. Scherzer, J. Appl. Phys. 20 (1949) 20.
|
