=================================================================================
In a simplified format for a perfect objective lens that does not have aberrations, the object wave o(r) at the exit face of an object is imaged by the objective lens into the image plane with two processes.
In the first process, the electron wave is diffracted into the back focal plane of the objective lens, mathematically described by a Fourier transformation,
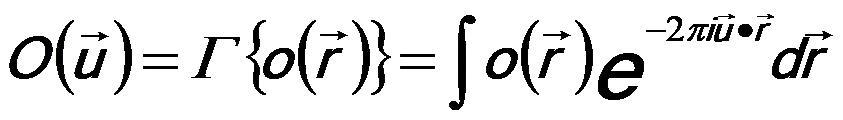 ---------- [2563a] ---------- [2563a]
where,
o(r) -- Also notated by ψ0(r),
O(u) -- The complex diffraction pattern, representing the object wave in Fourier space,
u -- The spatial frequency.
Due to the limited entrance aperture of the objective lens, the diffraction pattern also must be multiplied with the aperture function, A(u),
H(u) = O(u)A(u) ---------------------------- [2563b]
In the second process, all waves originating from the points in the Fourier space interfere with each other and result in image waves in the image plane, mathematically given by an inverse Fourier transformation,
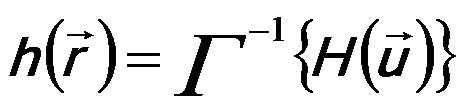 ------------------------ [2563c] ------------------------ [2563c]
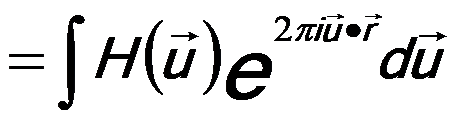 ------------------ [2563d] ------------------ [2563d]
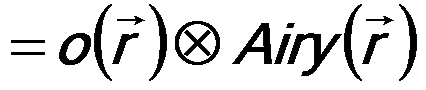 ------------------ [2563e] ------------------ [2563e]
Airy(r) = Γ-1{A(u)} is the Airy disk that gives the classical resolution limit indicated by Abbe's equation,
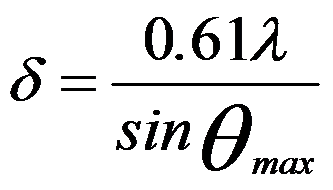 ------------------ [2563f] ------------------ [2563f]
To get the highest spatial resolution, the maximum diffraction
angle θmax should be recorded.
|
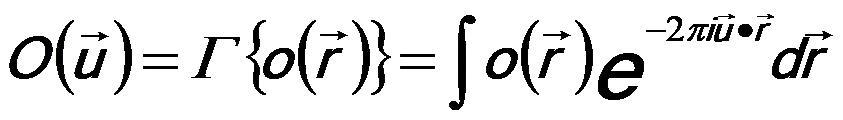 ---------- [2563a]
---------- [2563a]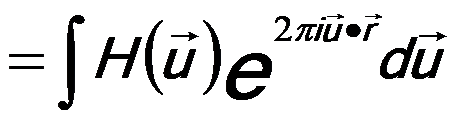 ------------------ [2563d]
------------------ [2563d]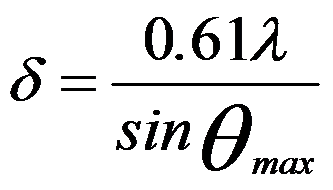 ------------------ [2563f]
------------------ [2563f]