=================================================================================
In one dimensional (1-D) FVdM (Frank and Van der Merwe) model in Figure 3492a, the atoms connected with the harmonic springs, representing a periodic potential, interact with each other with period b. The Hamiltonian may be taken to be,
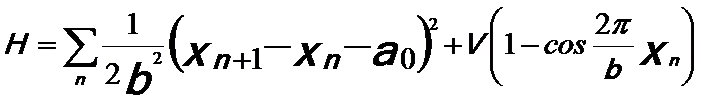 ------------------------ [3492a] ------------------------ [3492a]
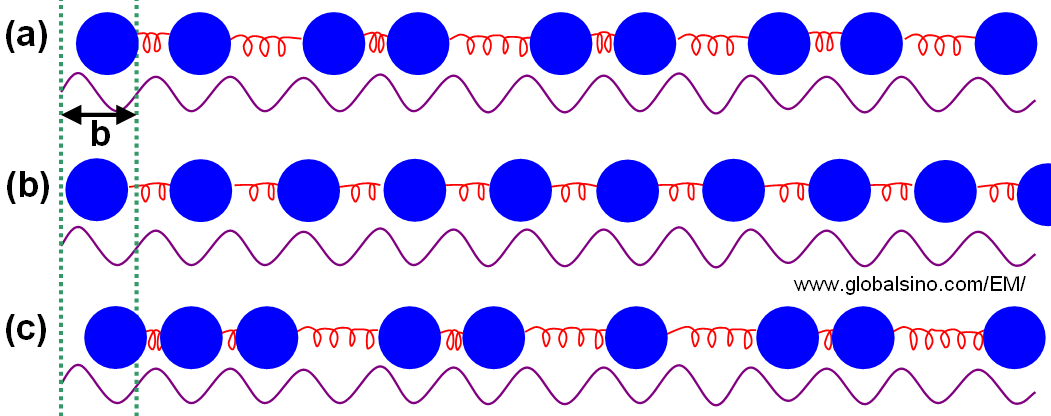
Figure 3492a. The 1-D FVdM model. The springs represent interactions between atoms:
(a) Commensurate structure, (b) incommensurate structure, and (c) chaotic structure.
where,
xn -- The position of the nth atom
In the case with a periodic potential V = 0, the harmonic term H would lead to a lattice constant a0, which, in general, would be incommensurable with b as shown in Figure 3492a (b). In a diffraction experiment one would observe Bragg spots (or sheets) at positions Q = 2πN/a0 (N is an integer). If the potential V is strong enough the lattice may tend to relax into a comrnensurate (C) structure where the average lattice spacing a is a simple rational fraction of the period b as shown in Figure 3492a (a).
Even in the case where the potential is not strong enough to force the chain into commensurability, the potential will still modulate the chain. That means, the atoms will move towards the potential minima. The average period may be close to a simple commensurate value, but still be incommensurate. In the most general incommensurate structure the position of the nth atom may be given by, [1 - 2]
xn = na + α + f(na + α) --------------------------- [3492b]
where,
α -- A phase
f -- Continuous and periodic number with period b
a -- The average distance between atoms (generally different from a0)
f -- The modulation of the chain due to the potential
However, chaotic structures cannot be described by Equation 3492b, where the diffraction pattern is not made up of well-defined Bragg spots.
[1] Janner A and Janssen T 1977 Phys. Rev. B 15 643.
[2] Aubry S 1979 Solitons and Condensed Matter Physics ed A R Bishop and T Schneider (Berlin: Springer-Verlag) p 264.
|
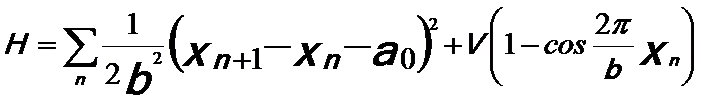 ------------------------ [3492a]
------------------------ [3492a] 