=================================================================================
Spherical aberration is the only form of monochromatic axial wavefront aberration produced by rotationally symmetrical surfaces centered and orthogonal in regard to the optical axis. The spherical attribute is due to this aberration being inherent to the basic optical surface - spherical - for object at infinity. Spherical aberration affects the entire image field, which makes its correction first priority. As shown in Figure 4335a, the parallel light or electrons passing through the periphery of the lens are focused more strongly than those passing through the centre and the circle of the least confusion (the best focus point) is located within the range of longitudinal spherical aberration. On the other hand, in Figure 4335a (b) the electrons leaving the point P of the object are refocused at the circle of the least confusion between P' and P'' instead of P' or P''. Consequently, in the image plane the point is imaged as a disk with radius (Δrs) given by,
 ---------------------------- [4335a] ---------------------------- [4335a]
where,
β -- The lens aperture.
Therefore, the point resolution deteriorates with increasing β.
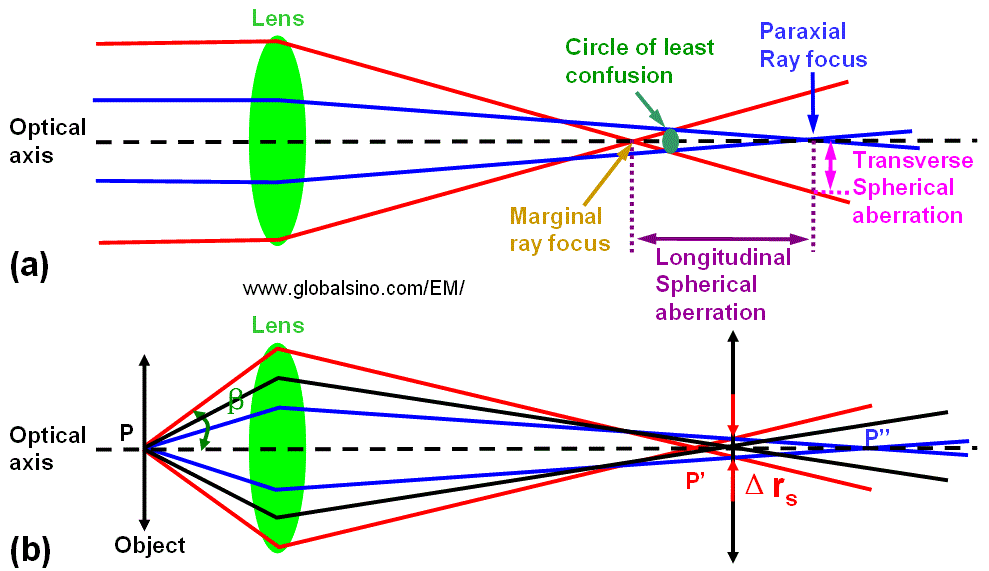
Figure 4335a.
Schematic diagram of
spherical aberration (SA): (a) Focusing
an initially parallel beam, and (b) Focusing electrons from an object.
Similar to the discussion regarding different accelerating voltages (the focal length at low accelerating voltages is much smaller than that at high accelerating voltages), for chromatic aberration, the light or electrons of different wavelength (or different energy E) are focused differently as shown in Figure 4335b. Different color represents different wavelength or energy of rays (light or electrons). There exists a point called the circle of least confusion, where chromatic aberration can be minimized and where the image plane locates.
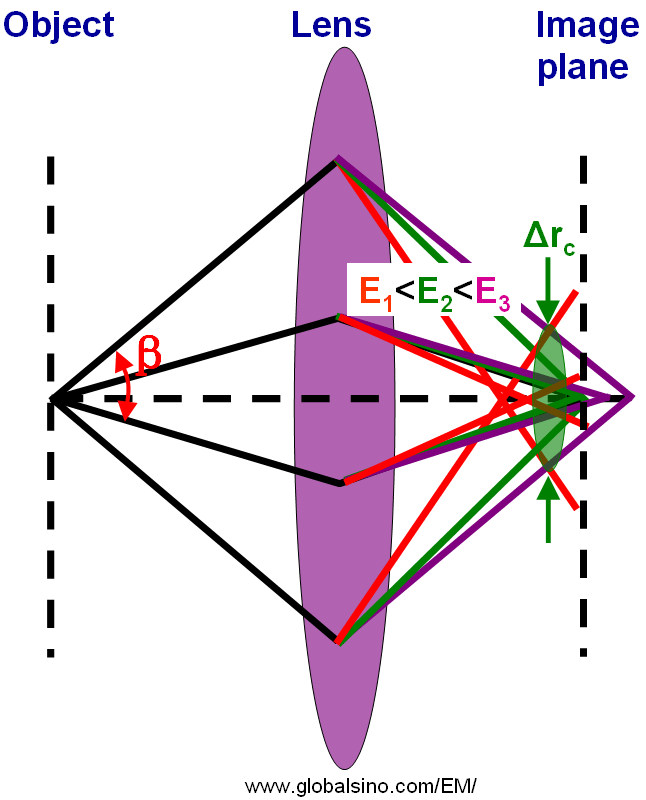
Figure 4335b. Schematic diagram of chromatic aberration.
In the case of chromatic aberration, the radius (Δrc) of the circle of least confusion can be given by,
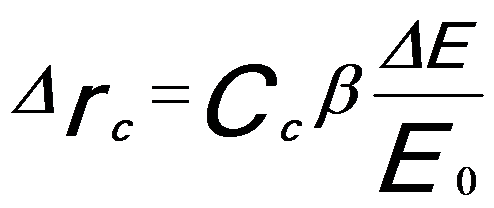 --------------------- [4335b] --------------------- [4335b]
The Cc coefficient is approximately equal to the focal length.
Equation 4335 indicates that the image of a single point will be a disk in the radius of Δrc, which limits the spatial resolution of the microscope.
When the lens presents different focal lengths depending on the planes that the electrons pass, astigmatism occurs. For instance, in Figure 1983, the electrons passing plane A are focused at point PA, while those passing plane B are focused at point PB.
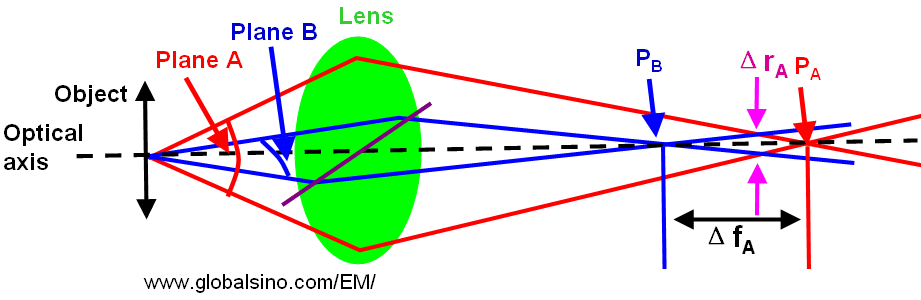
Figure 4335c. Schematic illustration of astigmatism.
In this case, the radius (ΔrA) of the circle of least confusion is given by,
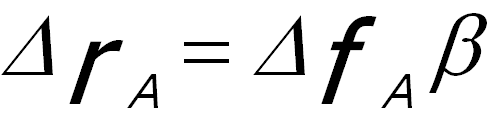 ------------------------ [4335c] ------------------------ [4335c]
where,
ΔfA -- The maximum difference in focal length.
|


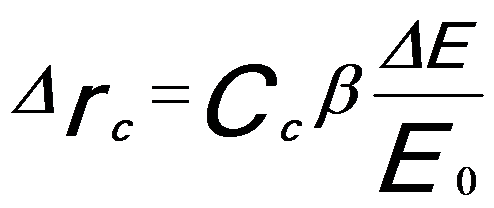 --------------------- [4335b]
--------------------- [4335b] 