=================================================================================
The cross section of elastic scattering of an electron, when divided by the actual area of an atom, gives the probability that a scattering event will occur.
Rutherford cross-section gives convenient formulas to calculate the elastic scattering angle and total elastic cross section so that it is often used to describe the elastic scattering of electron. However, its accuracy becomes worse in low-energy region or in high atomic-number materials.
Figure 4667a shows schematically electron scattering by an atom. Ω here is solid angle.
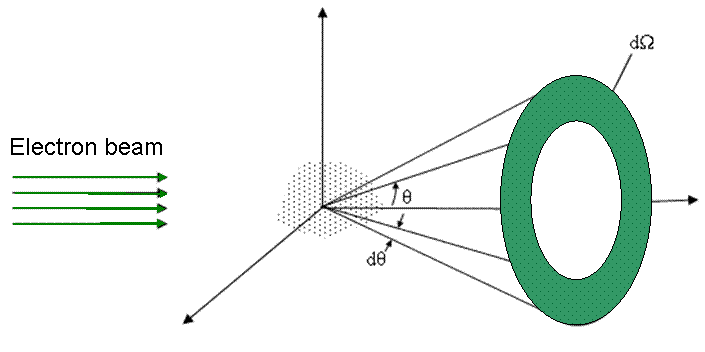
Figure 4667a. Schematic of electron scattering.
The cross-section of elastic-scattering is given by,
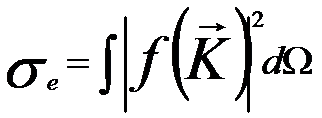 ------------------------------------------- [4667a] ------------------------------------------- [4667a]
where 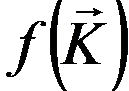 is a function, which defines the scattering properties by is a function, which defines the scattering properties by
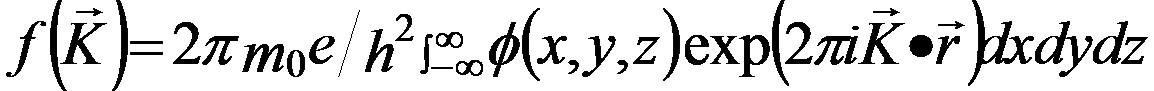 --[4667b] --[4667b]
The element of solid angle (Ω) can be written as,
dΩ= 2πsinθdθ --------------------------------------------------------------------[4667c]
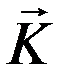 is the scattering vector, given in Figure 4667b. ki is the incident wave vector, ke the scatteredwave vector. For elastic scattering, |ke| = |ki| = 1/λ (λ is wavelength) and is the scattering vector, given in Figure 4667b. ki is the incident wave vector, ke the scatteredwave vector. For elastic scattering, |ke| = |ki| = 1/λ (λ is wavelength) and 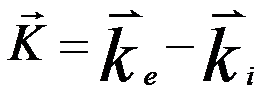 . The Bragg angle Φ and
the scattering angle θ are also shown in the figure. . The Bragg angle Φ and
the scattering angle θ are also shown in the figure.
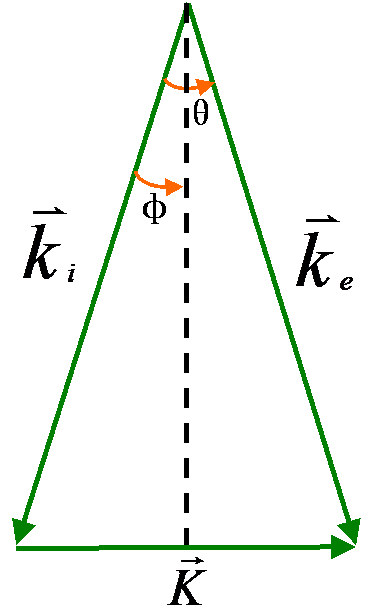
Figure 4667b. scattering vector for elastic scattering.
Based on Turner–Doyle scattering factors [1], σe can be plotted by the curve in Figure 4667c. On the other hand, by simple estimation, σe can be plotted by the straight line using Lenz model given by [2],
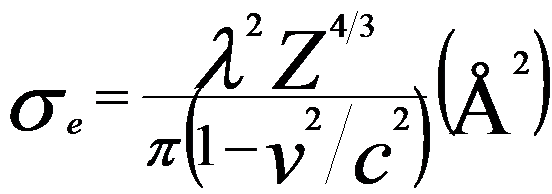 ------------------- [4667d] ------------------- [4667d]
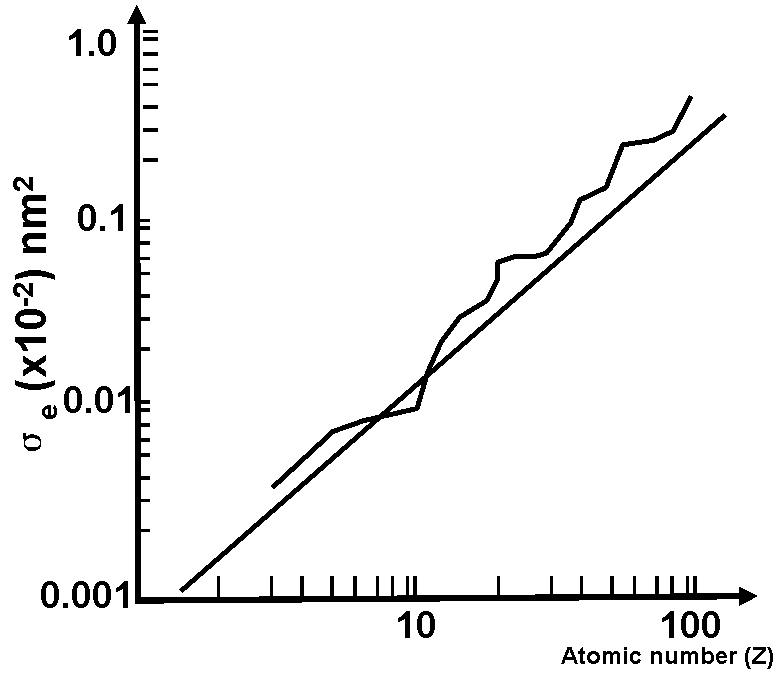
Figure 4667c. The elastic scattering cross-section σe plotted as a function of atomic number based on different models. The strength of the scattering increases with
atomic number. The two models are almost consistent. Both scales are logarithmic. [3]
Figure 4667d below shows the cross section of elastic scattering process in Al as a function of the incident electron energy at the scattering angles of ~ 0°. For comparison, the figure also shows cross sections for the various inelastic scattering processes.
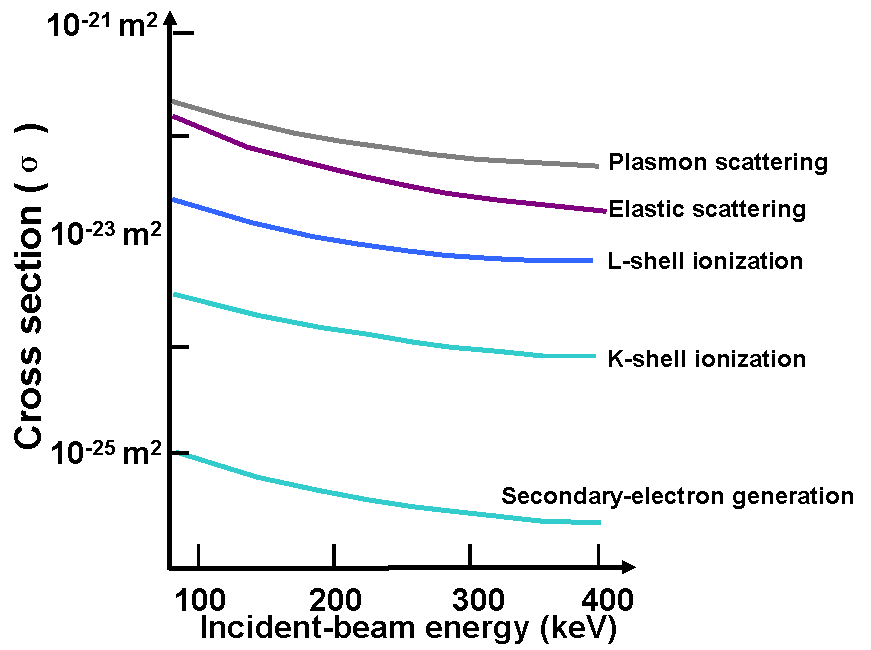
Figure 4667d. Cross sections for the elastic and various inelastic scattering processes in Al as a function of
the incident electron energy at the scattering angles of ~ 0°.
In ADF (Annual Dark Field) imaging, assuming the detector has a large outer
reciprocal radius, then the cross-section of elastic scattering can be expressed by the empirical relation,
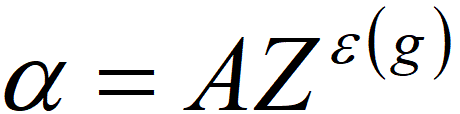 ------------------------- [4667e] ------------------------- [4667e]
where,
g --- The inner reciprocal radius of the annular detector.
A -- The cross section for hydrogen.
Z -- The atomic number of the detecting element.
ε -- The exponent, which depends on g. (see page4788)
The elastical scattering cross-section
for the electrons scattered by an atom to the corresponding scattering angles of the
HAADF detector can also be given by,
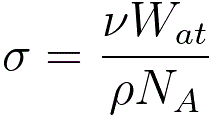 ------------------------- [4667f] ------------------------- [4667f]
where,
ν -- fraction of electrons scattered onto the HAADF-STEM detector per
nanometer of sample thickness,
Wat -- atomic mass,
ρ -- atomic density,
NA -- Avogadro’s number.
[1] Humphreys, C. J., Hart-Davis, A., and Spencer, J. P. (1974). Optimizing the signal/noise in the dark field
imaging of single atoms. Proc. 8th Int. Congr. Electron. Microsc., Canberra, p. 248.
[2] Lenz, F. (1954). Zur Streung mittleschneller elektronen in klienste Winkel. Z. Naturforsch. 9A, 185. |