This book (Practical Electron Microscopy and Database) is a reference for TEM and SEM students, operators, engineers, technicians, managers, and researchers.
 

=================================================================================

The general procedure to define a Burgers vector b of a dislocation in a crystal is the Burgers circuit construction using finish-start/right-hand (FS/RH) (or called end-start/right-hand (ES/RH)) convention.

As shown in Figure 3460, in a crystalline plane perpendicular to the sense vector, the Burgers circuit in a perfect lattice can be created by a series of discrete steps from a lattice site to the next in the clockwise direction. The circuits on the left- and right-hand sides of the schematic illustration are represented by the lime arrows and the green dots. In the circuit on the left, the drawing first starts by 3 steps towards the top, then by 4 steps towards the right, then by 5 steps towards the bottom, then by 4 steps towards the left and finally, by 2 steps towards the top and thus steps back to the start site. Note that the steps at the top is the same as that at the bottom (L₁ = 4 here) and the total steps on the left of each circuit is the same as that on the right too (i.e. L₂ = 5 here). Both the start (S) and end (E) points (indicated by the same color, i.e. red) locate at the same lattice site in a perfect lattice. However, when a similar circuit (meaning the same L₁ and L₂) is drawn around a dislocation as shown in the second circuit, a closure of the Burgers circuit fails, that is the end step does not go back to the start site (indicated by different color, i.e. red and blue). The Burgers vectors are conventionally drawn from the start site to the end site. The same Burgers vectors can be obtained no matter how many steps L₁ and L₂ are, respectively.

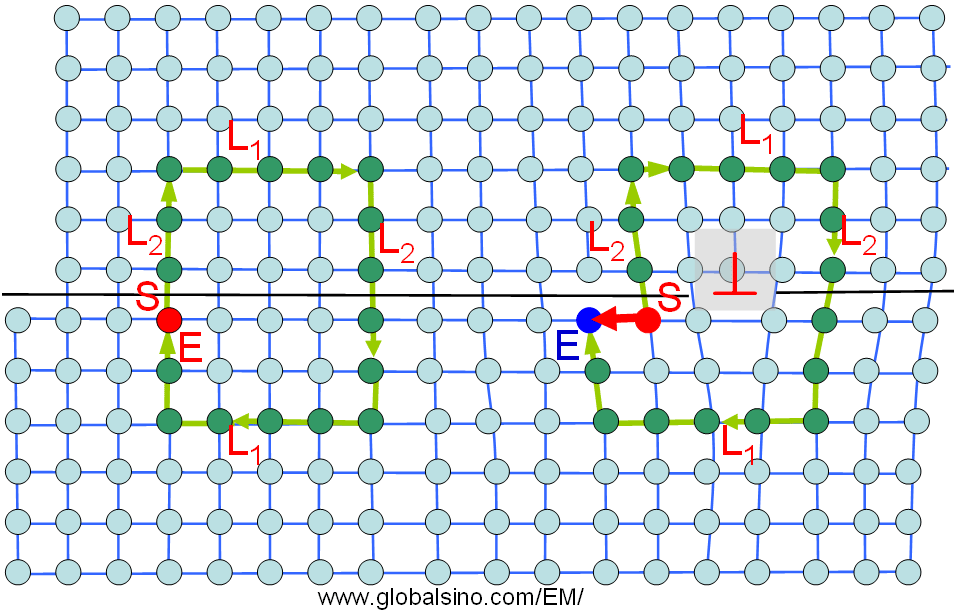
Figure 3460. Burgers circuit and Burgers vector.

Note that when the sense vector is reversed, the resulting Burgers vector is also reversed. Therefore, one of the characteristics of the dislocations is represented by the cross product of the sense vector and the Burgers vector, always pointing to the extra half plane of atoms that defines the edge dislocation: 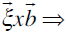extra half plane, regardless of which direction the sense vector points as shown in page3459.