This book (Practical Electron Microscopy and Database) is a reference for TEM and SEM students, operators, engineers, technicians, managers, and researchers.

=================================================================================

When a fine probe irradiates an insulator at normal incidence, the surface potential is no longer uniform over the surface but it is a function of the lateral co-ordinate r, V(r,0), as shown in Figure 4565, because charging can induce electrostatic stress. This surface potential is a function of the increase in positive and negative charges and their redistribution into the specimen. The negative charge distribution is proportional to 1 − η₀ developed down to the maximum penetration depth of the primary electrons (PEs) and spreads over a more or less spherical volume of approximate diameter R₀. η is the backscattering coefficient of electrons. One strongly non-uniform positive charge layer at thickness t results from the lateral distribution of SE1 released at the surface by the primary electrons (PEs), δ_P, while the other distribution of SE2 is generated by backscattered electrons (BSEs), δ_B. SE1s are generated within a disc determined by the incident spot diameter, d_P, so that the associated positive charges are highly concentrated in a very small volume. Around the impacted disc, the electric field is centrifugal and the surface potential is positive. The whole system is negatively charged when δ₀ + η₀ < 1. Here, δ is secondary electron emission yield. In such a state, the surface potential V(x) changes the sign with radii (r) and the electric field changes direction. As suggested by Cazaux[3], Figure 4565 (b) shows the change in direction of the electric filed component (F_r) when δ₀ + η₀ < 1 (upper and front view of the surface). The approximate shape of the surface potential function, V(r,0) when δ₀ + η₀ < 1 (green curve). When δ₀ + η₀ > 1, this function is completely positive and the electric field remains centrifugal. This principle may be applied to explain some ring features obtained under short pulse and focused irradiations. An example is shown in Figure 4565 (a).

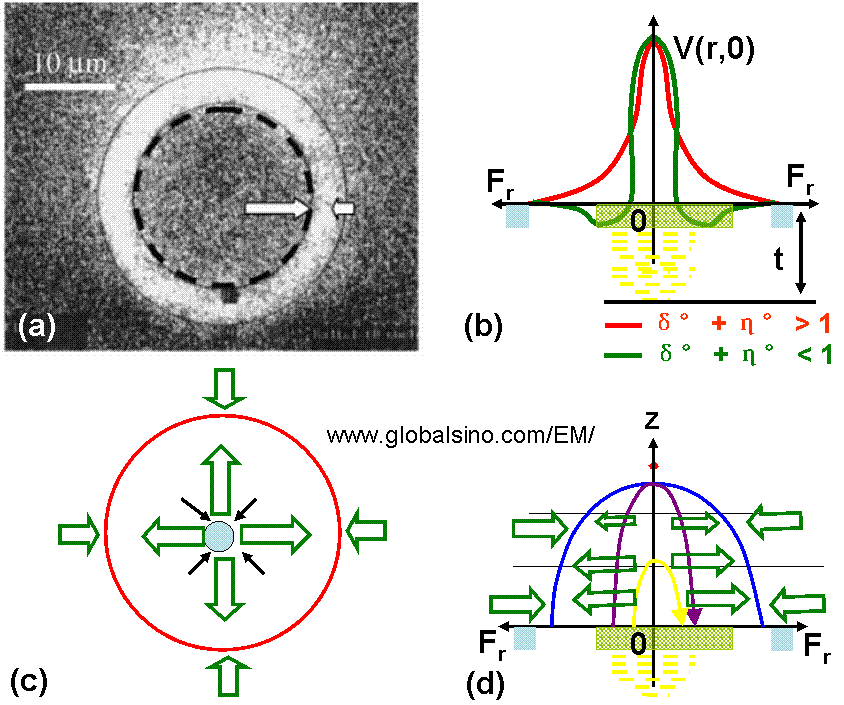
Figure 4565. (a) Ring shape feature resulting from the injection of 12 pC into polyethylene at 30 keV (adapted from [1]). (b) Calculated radial potential function, V(r,0), when δ₀ + η₀ > 1 (red curve) and δ₀ + η₀ < 1 (green curve) (adapted from [2]). (c) Calculated radial field component F_r (open green arrows) induced by a focused probe when δ₀ + η₀ < 1. (d) Top view of the surface when δ₀ + η₀ < 1. Front view with the SE trajectories of the most energetic SE (violet arrow) and the re-attraction of the less energetic SE (yellow arrow).

[1] Mady, F., Renoud, R., Attard, C., Bigarré, J., Ganachaud, J.-P. & Hourquebie, P. (2002) Interpretation method for mirror experiments based on a Monte Carlo implantation model. Eur. Phys. J. Appl. Phys. 20, 41–53.
[2] Cazaux, J. (2005) Recent developments and new strategies in scanning electron microscopy, Journal of Microscopy, 217, 16–35.
[3] Cazaux, J. (2004) About the role of the various types of secondary electrons on the performance of LVSEM. J. Microscopy 214, 341–347.