=================================================================================
The single scattering
distribution of electrons interacting with matter is proportional to Im(−1/ε) where ε is the dielectric function which depends on the energy and the momentum transfer. Based on the cross-section for inelastic scattering, the single scattering distribution (SSD) can be expressed as,
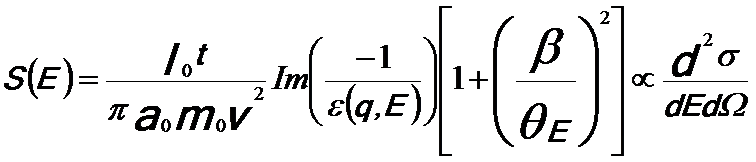 ------------------------------ [4356a] ------------------------------ [4356a]
Where,
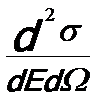 -- See page4360; -- See page4360;
v -- The speed of the incident electron;
I0 -- The zero-loss intensity;
a0 -- The Bohr radius;
m0 -- The resting mass of the electron;
t -- The specimen thickness;
ε(q,E) -- The dielectric function;
q -- The momentum transfer;
E -- The loss energy by inelastic scattering;
β -- The collection semi-angle;
θE -- The characteristic angle of
inelastic scattering.
For small q, ε(q,E) varies very slowly with q and thus it can be replaced by ε(E).
The dielectric function ε is used to describe both single and collective excitations induced by interaction of incident electrons with materials [1]. According to Drude model [2,3], the energy loss function (ELF) for a bulk plasmon can be given by,
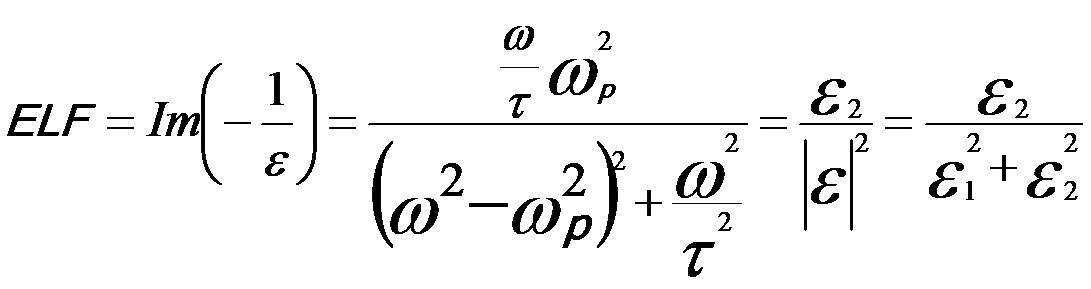 ----------------------- [4356b] ----------------------- [4356b]
where,
ωp -- Bulk plasmon frequency for collective excitation of free electrons;
τ -- Constant
related to the life time of the excitation;
ε1 -- The real part
of the dielectric function;
ε2 -- The imaginary part
of the dielectric function.
Figure 4356a presents the ELF and ε1 and ε2 as a function of energy loss. The arrows show
the plasmon peaks and the corresponding ε1 around their values close to 0.
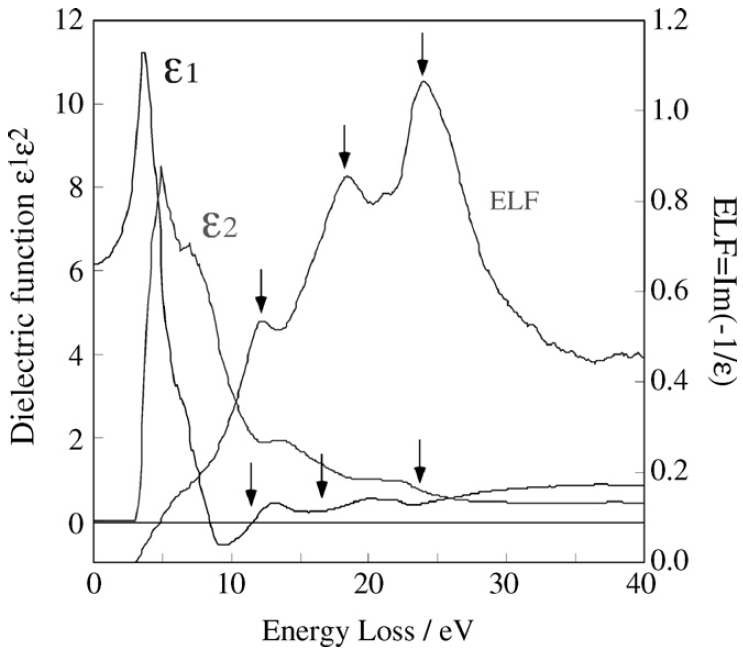
Figure 4356a. The ELF and ε1 and ε2 as a function of energy loss. [4]
SSD spectra can be extracted from experimental spectra by deconvolution of elastic/quasi-elastic phonon and multiple scattering effects. For instance, this deconvolution can be done by removing multiple scattering with Fourier-log deconvolution method, and then the SSD is given by,
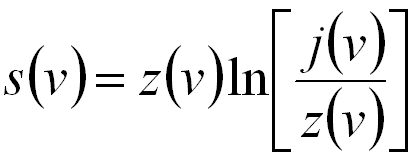 ------------- [4356c] ------------- [4356c]
where,
j(v) -- The Fourier transforms of the recorded EELS data.
z(v) -- The Fourier transforms of the zero-loss spectrum in EELS.
For some materials (especially wide band gap materials), in higher energy-resolution EELS measurements, the band gap (Eg) can be determined by eye observation of the SSD spectrum that is obtained from low-loss spectra. In this case, Eg is defined as the energy corresponding to the first onset in the spectrum, for instance, 0.67 and 1.12 eV for Ge and Si respectively, in the schematic spectra in Figure 4356b.
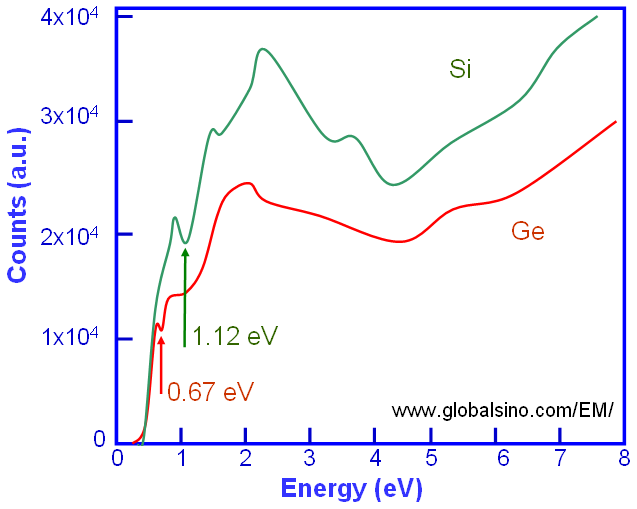
Figure 4356b. Schematic illustration of Si and Ge SSD spectra in the low-energy range.
On the other hand, the band gap can also be determined based on Bethe’s theory. In this case, the SSD spectrum is described to be proportional to the product of the joint density of states (JDOS). Here, the JDOS is given by,
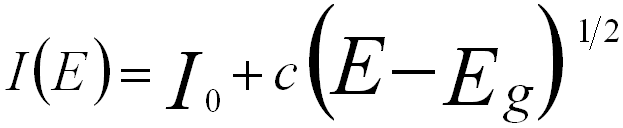 for a direct band gap, ------------- [4356d] for a direct band gap, ------------- [4356d]
and,
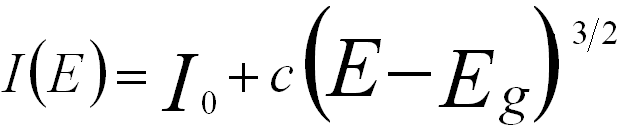 for an indirect band gap ------------- [4356e] for an indirect band gap ------------- [4356e]
where,
I0 and c -- The constants.
E -- The energy loss.
Therefore, Eg can be extracted by fitting the single scattering spectrum using Equations [4356d] and [4356e].
Figure 4356c shows the band gap determination of the HfO2 layer in a Si/SiO2/HfO2/poly-Ge stack by using Equation 4356d (direct band gap [Eg = 5.26 eV] for HfO2).
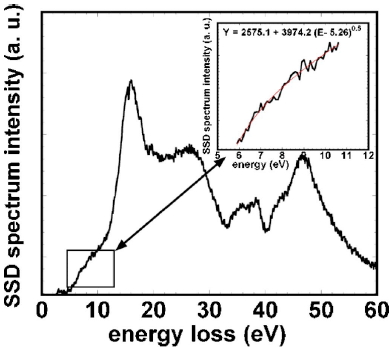
Figure 4356c. Band gap determination of the HfO2 layer in a Si/SiO2/HfO2/poly-Ge stack. Adapted from [5]
If the SSD is known, then optical
techniques such as Kramers–Kronig analysis can be
applied to determine the dielectric function, reflectivity,
absorption, etc. [7]
For more accurate calculations, it is important to note that SSDs contain bulk plasmon-loss spectra as well as surface losses, especially when the specimens are very thin. Therefore, the SSD can be given by,
ISSD(E,t) = Ib(E,t) + Is(E,t) ------------- [4356f]
where,
Ib(E,t) -- The bulk loss.
Is(E,t) -- The surface loss.
t -- The thickness.
The surface plasmon-loss (Is) has dependence on TEM-specimen thickness only when the specimen is extremely thin (e.g. <10 nm in general). The bulk loss is given by,
Ib(E,t) = t•[Ip(E) + Iint(E)+ICh(E)] ------------- [4356g]
where,
Ip -- The bulk plasmon-loss spectrum unit thickness.
Iint -- The interband transition spectrum unit thickness (the region of 0 to 10 eV).
ICh -- The Cherenkov radiation in unit thickness (the region of 0 to 10 eV).
Table 4356. Electron scattering versus TEM sample thickness.
Electron scattering |
TEM sample thickness |
Single scattering |
≤ 20 nm |
Multiple scattering |
> 20 nm |
Mkhoyan et al. [6] presented SSDs obtained from experimental EELS data from silicon (Si) specimens with four different thicknesses as shown in Figure 4356d. The band gap or electronic states in the gap presented in the figure were inaccurate due to the low energy-resolution. In their measurements, the energy resolution was 0.7 eV, and the channel size 0.22 eV so that it was impossible to quantify features located below 2 eV.
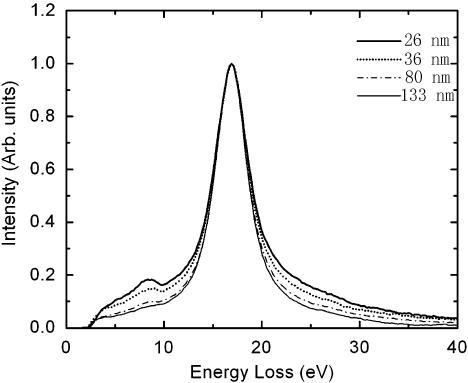
Figure 4356d. SSDs obtained from experimental EELS data from Si specimens with four different thicknesses.
Adapted from [6]
It is very common that SSD is obtained by subtracting the original spectrum with a power-law fitting of the ZLP tail performed in Gatan Digital Micrograph software.
If the noise in an EELS profile is large , a practical procedure to study the SSD is:
i) Use Savitzky-Golay filter to smoothen the raw spectra.
ii) Compute the first derivative.
iii) Find the useful information, for instance, related to electronic structures of the materials.
[1] Ritchie R.H. and Howie A., Phil. Mag. 36 (1977) 463.
[2] Raether H., Springer Tracts in Modern Physics (Springer Verlag, 1980) p. 88.
[3] Pines D., Rev. Mod. Phys. 28 (1956) 184.
[4] Takanori Kiguchi, NaokiWakiya, Kazuo Shinozaki, Toyohiko J. Konno, Valence-EELS analysis of local electronic and optical properties of PMN–PT
epitaxial film, Materials Science and Engineering B 161 (2009) 160–165.
[5] Marie C. Cheynet, Simone Pokrant, Frans D. Tichelaar, and Jean-Luc Rouvière, Crystal structure and band gap determination of HfO2 thin films, Journal of Applied Physics 101, 054101 (2007).
[6] K.A. Mkhoyan, T. Babinec, S.E. Maccagnano, E.J. Kirkland, and J. Silcox, Separation of bulk and surface-losses in low-loss EELS
measurements in STEM, Ultramicroscopy 107 (2007) 345–355.
[7] R.F. Egerton, Electron Energy-Loss Spectroscopy in the
Electron Microscope (Plenum Press, New York, 1996).
|