=================================================================================

There are many different methods which can be used to determine the lattice parameters of the unit cells of crystals, based on different known information, software and TEM samples:
        i) An efficient way to determine the lattice parameters is by the acquisition of three lattice covectors whose linear combinations span the entire reciprocal lattice, [2] if high angle tilt (e.g. a total range of tilt angle >36°) in TEM can be performed. For instance, a procedure which can be employed to determine the lattice parameters of nanocrystals is:
        i.a) Find a nanocrystal with a certain tilting axis;
        i.b) Tilt the TEM sample in positive and negative directions around the tilting axis and thus find a series of reciprocal planes;
        i.c) Determine the crystal structure and the lattice parameters of the reciprocal lattice from the seven crystal families based on the obtained numbers above;
        i.d) Convert the reciprocal lattice parameters to lattice parameters in real space.
For instance, this method was used to determine the unknown structure of the new hydrocarbon nano-crystals, by energy-filtered electron diffraction, as a triclinic unit cell with lattice parameters of a = 6.03 Å, b = 6.23 Å, c = 13.86 Å, α = 87.26 °, β = 106.69 °, and γ = 119.01 ° [1].
        ii) Based on the same principle above, lattice parameters can be determined by following the lattice-fringe visibility bands.
        iii) Once the space group has been identified, systematic indexing of each zone axis can be applied to obtain the lattice constants.
        iv) Determine lattice parameters using CBED technique. Especially, by measuring the radius of the FOLZ (first HOLZ) ring of CBED patterns (e.g. the [0001] CBED pattern in Figure 3496), the length of the c-axis can be calculated by (see page3902 for details),
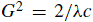         -------------------------------------- [3496]
where,
          G -- The radius of the FOLZ ring.
          λ -- The electron wavelength.

Figure 3496. Whole-pattern symmetry (HOLZ) of the [0001] CBED pattern of T1 (Al2CuLi) crystals. Adapted from [3]

Note that the maximum achievable sample-tilt angles in TEMs are normally smaller than ±30° with commercial single- and double-tilt holders. These angles are barely higher than the tilt required for lattice parameter measurements as indicated by the standard indexed diffraction patterns for fcc, bcc, and hcp crystals.

[1] Structural study of new hydrocarbon nano-crystals by energy-filtered electron diffraction, J. S. Wu, N. Melcer, W. P. Sharp, M. O’Keeffe, J. C. H. Spence, O. M. Yaghi, Ultramicroscopy 98 (2004) 145–150.
[2] P. Fraundorf, Ultramicroscopy 6, 227 (1981).
[3] Kenneth S. Vecchio and David B. WILLIAMS, Convergent Beam Electron Diffraction Analysis of the T1 (Al2CuLi) Phase in Al-Li-Cu Alloys, Metallurgical Transactions A, 19A, 1988-2885, (1988).