EELS of Carbon (C) - Practical Electron Microscopy and Database - - An Online Book - |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Microanalysis | EM Book https://www.globalsino.com/EM/ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Among all the spectroscopy techniques, most early core excitation spectroscopy applied to polymer, particularly at the C 1s core edge, had been performed by EEL spectroscopy. For carbon, EELS analysis can be used to characterize its band gap, inter-band transition, and density of state, and quantify the sp3 fraction versus sp2 in amorphous diamond. Table 4709a lists the typical energy-loss peaks of the various forms of carbon. The cross-section of carbon K shell ionization are of the order of 1 pm2 per atom. Table 4709a. Typical energy-loss peaks of the various forms of carbon.
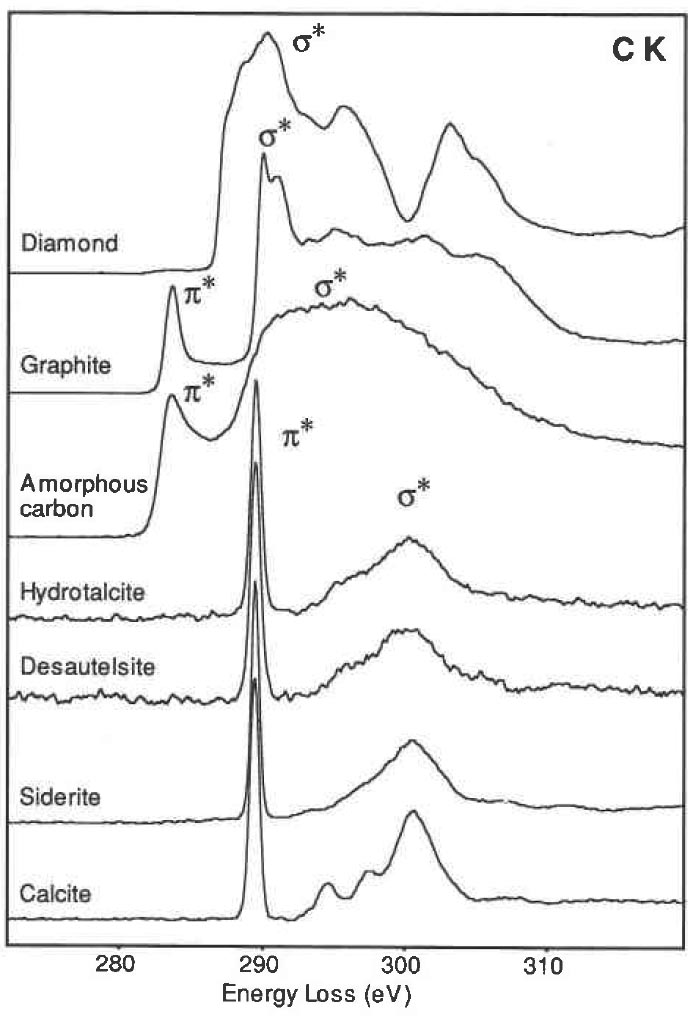
Figure 4709a shows carbon (C) K edge from materials containing the carbonate anion (calcite, siderite, desautelsite, and hydrotalcite) and three allotropes of C (amorphous , graphite, and diamond). EELS profiles of amorphous C and graphite present basically the same edge shapes, with the first peak at 285 eV induced by transitions to the π* molecular orbital due to the presence of sp2 bonding, and the second, more intense peak at 290 eV induced by transitions to σ* orbitals. In diamond the bonding between the C atoms can be interpreted in terms of tetrahedrally directed sp3 hybrid orbitals, and the first peak with a maximum at 292.6 eV is identified as arising from transitions to molecular orbitals of σ* character.
Figure 4709a. Carbon K edge from calcite, siderite, desautelsite, hydrotalcite, amorphous, graphite, and diamond.
Furthermore, amorphous sp2 bonded carbon is also responsible for a relatively large feature at approximately 6 eV in EELS [4]. Figure 4709b shows the comparison of EEL spectra between amorphous diamond and nanocrystalline diamond.
Figure 4709b. Comparisons of (a) plasmon and (b) core-loss in the energy range of 200 - 500 eV (a) between amorphous diamond and nanocrystalline diamond. Figure 4709c shows the high-energy-resolution EELS spectra of plasmon region and core-loss in the energy region of 280 to 298 eV for C60 fullerene, and amorphous and crystalline diamond.
Figure 4709c. High-energy-resolution EELS spectra of (a) plasmon region and (b) core-loss in the energy region of 280 to 298 eV for C60 fullerene, and amorphous and crystalline diamond. The loss function (Im[-l/ε]) can be obtained by removing the contribution of multiple scattering from the EEL spectra of plasmon region in Figure Figure 4709c (a) using the Fourier-log deconvolution method. An optical absorption method can directly provide the imaginary part of the dielectric function, ε2, associated with a single electron excitation of an interband transition, while EELS cannot directly give ε2. Based on the obtained loss function, the real part (ε1), and the imaginary part (ε2) of the dielectric function for the crystalline and the amorphous diamond are extracted using Kramers-Kronig analysis as shown in Figure 4709d. Table 4709b lists the onset energy (indicating the band gap energy) and the peaks in the imaginary spectrum obtained from Figure 4709d and the original interband transitions.
Figure 4709d. Real part (ε1), and the imaginary part (ε2) of the dielectric function for (a) crystalline and (b) amorphous diamond. Table 4709b. Onset energies (band gap energies), peaks in the imaginary spectrum in Figure 4709d and the original interband transitions.
For carbon nanotubes and graphite, as shown in Figure 4709e, not only does the core electron EELS spectra for the nanotubes shift to lower energies from those of graphite due to their lower-dimensional feature and thus due to the lower carrier densities and conductivities than graphite, but also the EELS on both the tubule bundle and graphite are sensitive to the incident electron beam along their crystalline axis. Figure 4709e. Core electron EELS spectra for both nanotubes and graphite with the incident electron in TEM along their different crystal orientations.
Adapted from [1]
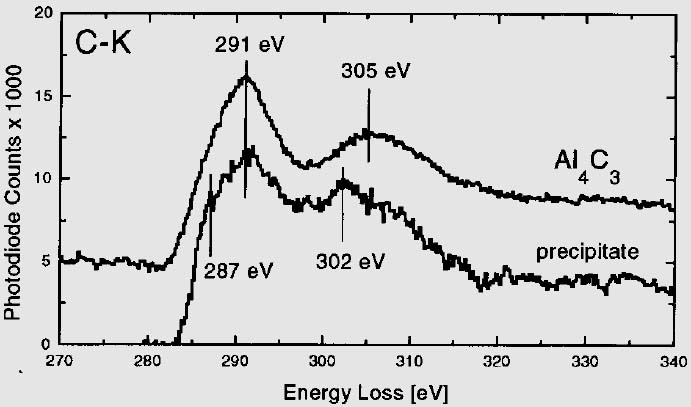
Figure 4709f shows the C K ionization edges of Al4C3 and of a precipitate in C/Mg-Al composites with its maximum peak at ~ 291 eV. For the precipitate phase, however, starting at 287 eV the rising slope decreases slightly on the left of the peak of 291 eV. Moreover, another broader peak appears at about 303.5±1.5 eV with a energy difference of ~ 3 eV between the two cases.
Figure 4709f. C K ionization edges of Al4C3 and of a precipitate in C/Mg-Al composites. [2]
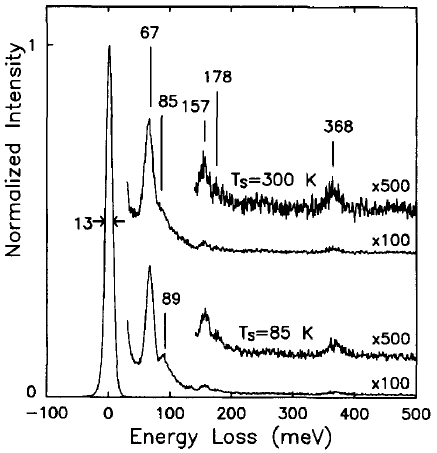
Brown and Ho [3] used an EELS spectrometer with an incident electron energy of 10 eV, consisting of a double-pass cylindrical monochromator and single-pass cylindrical analyzer, to analyze the interaction between methyl chloride and Si( 100) 2 x 1. Figure 4709g shows the EEL spectra obtained after 1 L exposures of methyl chloride (CH3CI) onto the Si(100) surface held at 85 and 300 K. The origin of the peaks, related to the existence of molecularly adsorbed species, is listed in Table 4709c.
Figure 4709g. The EEL spectra obtained after 1 L exposures of methyl chloride onto the Si(100) surface held at 85 and 300 K. [3] Table 4709c. The origin of the peaks in Figure 4709g.
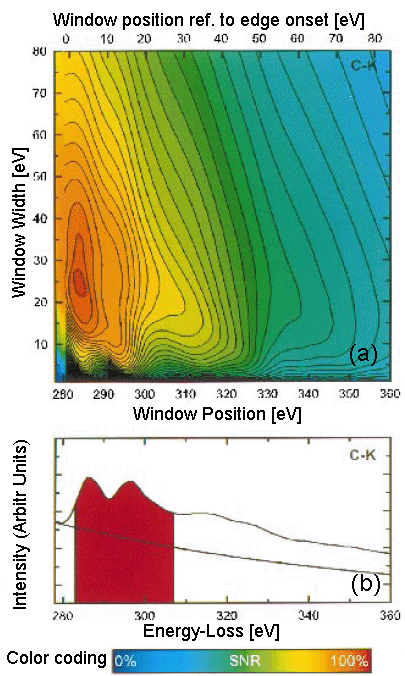
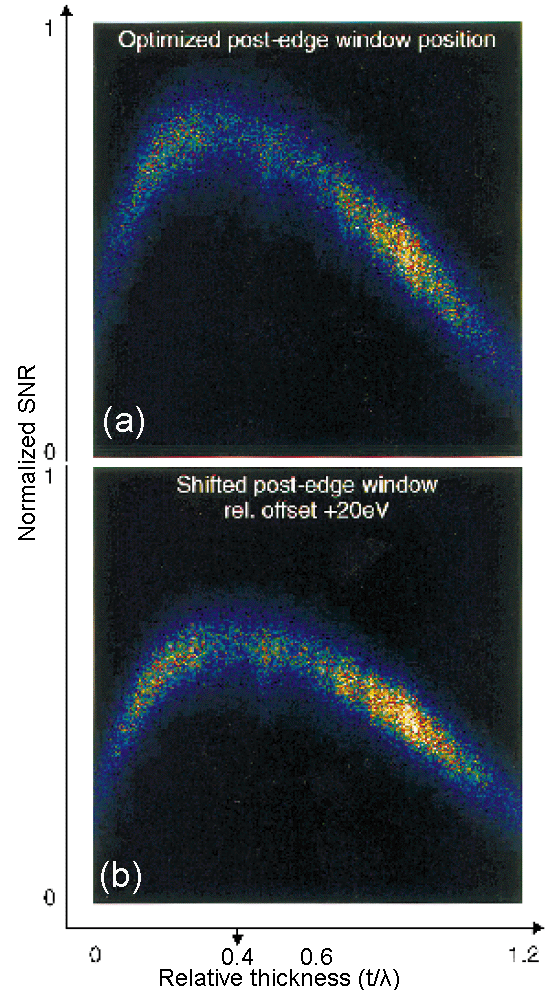
Carbon K-edge shows very sharp onsets with high intensity piled up at the threshold energies as shown in Figure 4709h (b). The K-edge provides an opportunity of large edge signals and small background extrapolation error h. Because a fast decline of the cross-sections above ~ 30 eV of the onset toward the background shown in Figure 4709h (b), the simulation suggests a window width of ~ 30 eV is an optimized window for EELS signal collection as indicated in Figure 4709h (a).
Figure 4709h. Contour plot representation of the Signal to noise ratio (SNR) optimum for carbon element and edge shape as a function of post-edge window position and window width of signal, obtained by simulation. The red shaded areas in (a) correspond to the highest SNR (100%) which can be obtained. Simulation condition: energy of the incident electron beam is 200 keV and collection angle is 7.6 mrad [1]. Figure 4709i shows two correlation plots calculated from filtered image series taken with a 25 eV slit at conditions in three window method: pre-edge 1 = 225 eV, pre-edge 2 = 265 eV and with post-edge = 295 eV and with energy window = 315 – 295 = 20 eV, respectively. The optimal specimen thickness around t/λ = 0.4 for carbon under the condition of 200 keV (energy of the incident electron beam) and 7.6 mrad (collection angle). Extremely thin specimen areas cause the SNR to drop due to increased noise, whereas plural scattering in thick areas decreases the signal relative to the background. A shift of the post-edge window by 20 eV (Figure 4709i (b)) lowers the maximum SNR value of approximately 25% as a fact of a larger background extrapolation error (h) and a decreased signal.
Note that EELS measurement can be done in electron diffraction mode in TEM. In this mode, the beam illumination area can be very large if the material non-uniformity is not an issue. Therefore, carbon contamination and beam damage can be minimized because when the beam is enlarged the beam current density can be very small. The plasmon energy loss can experimentally provide indirect semi-quantitative information because the free-electron density n changes with the chemistry or bonding state of the TEM specimen. The empirical plasmon peak position (Ep) can be given by, Ep = Ep(0) ± C(dEp/dC) -------------------------------- [4709] Therefore, once Ep is obtained from EELS measurement, then C can be evaluated. For instance, as shown in Figure 4709j, empirical sp2/sp3 ratios in amorphous carbons were evaluated based on Equation 4709 and the relative intensity of k-edge 1s to π* transition [6-10]. Figure 4709j. Fraction of sp3 bonding as a function of the bulk plasmon energy. [6] However, in many cases, carbon is one of the most difficult contaminants, incorporated from fab-environment, to be detected by analytical TEM such as TEM-EDS and TEM-EELS techniques because of two reasons:
[1] Optimization of the signal to noise ratio in EFTEM elemental maps with regard to different eonization edge types, Kothleitner, G and Hofer, F, Micron, 29, 5, pp. 349–357, (1998). |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||